) to partition geometric entities of a mesh by creating at least one new geometric entity for the elements enclosed in the specified ball, as seen in Figure 8-88.
) to partition geometric entities of a mesh by creating at least one new geometric entity for the elements enclosed in the specified ball, as seen in Figure 8-88.
 |
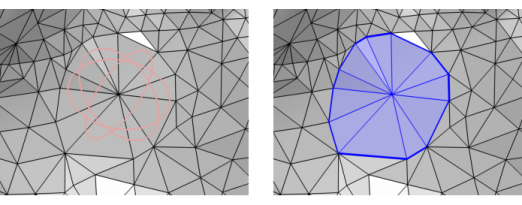
Note that partitioning a mesh can modify the number of geometric entities. Thus when you are adding this operation to a meshing sequence that is conforming with the component’s geometry, a new meshing sequence that is defining its own geometric model is automatically created, and the Partition with Ball node is added to this new sequence. For more information, see The Mesh Node.
|
) node, select one or several entities in the Graphics window, then choose one of the following:|
•
|
Right-click in the Graphics window to open The Graphics Context Menu. Select Partition with Ball (
 ) from the Booleans and Partitions menu. |
|
•
|
|
•
|
|
•
|
Choose Entire geometry to divide all geometric entities according to the specified ball.
|
|
•
|
Choose Domain, Boundary, or Edge to specify the domains, boundaries, or edges, respectively, that you want to partition or choose a named selection to refer to a previously defined selection. Use All domains, All boundaries, or All edges to select all entities of the specified dimension.
|
 |
|
) on 
) from the