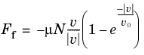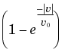Joints
About Joints
A joint is used to allow a certain type of relative motion between the two components it connects. A joint is a global feature that needs two attachments, one from each component. One attachment acts as a source and the other as a destination.
The two attachments belonging to a joint can be Attachment features, Rigid Domain features, or a combination of the two. The source attachment can also be set to be either fixed or to have a given Base motion. In the case of a fixed attachment, it cannot translate or rotate. This avoids the modeling of extra fixed rigid domains when a structure is “grounded.” The base motion is a generalization of the fixed attachment, where the environment to which it is attached can have a prescribed displacement, velocity or acceleration.
The source attachment moves independently in space whereas the destination attachment is constrained to follow the source attachment allowing for some relative degrees of freedom in the form of translation or rotation. The relative degrees of freedom are determined by the type of joint. In each joint, the relative degrees of freedom are represented by ODE variables.
The degrees of freedom which are constrained in a joint can be either rigidly constrained, or contain some relative elastic displacement.
The rest of this section has these topics:
•
Joint Types and Degrees of Freedom
•
Selecting Attachments
•
Joint Axis and Local Coordinate System
•
Positioning the Joint Center
•
Constraints
•
Locking
•
Springs and Dampers on Joints
•
Elasticity in Joints
•
Prescribed Motion
•
Applied Forces and Moments on Joints
•
Friction
•
Computing Joint Forces and Moments
•
Initial Values of Joint Degrees of Freedom
Joint Types and Degrees of Freedom
Table 2-1 lists the joint types for 3D models based on the possible relative degrees of freedom.
Table 2-1: Joint types and degrees of freedom in 3D
Joint type
Total degrees of freedom
translational degrees of freedom
rotational degrees of freedom
Prismatic Joint
1
1
0
Hinge Joint
1
0
1
Cylindrical Joint
2
1
1
Screw Joint*
1*
1
1
Planar Joint
3
2
1
Ball Joint
3
0
3
Slot Joint
4
1
3
Reduced Slot Joint
2
1
1
Fixed Joint
0
0
0
Distance Joint**
5
2**
3
Universal Joint
2
0
2
* For a Screw Joint, the two degrees of freedom are linearly dependent.
** For a Distance joint, all three translational degrees for freedom are not independent.
Table 2-2 lists the available joint features for 2D models:
Table 2-2: joint Types and degrees of freedom in 2D
Joint type
Total degrees of freedom
translational degrees of freedom
rotational degrees of freedom
Prismatic Joint
1
1
0
Hinge Joint
1
0
1
Reduced Slot Joint
2
1
1
Fixed Joint
0
0
0
Distance Joint**
2
1**
1
** For a Distance joint, both translational degrees for freedom are not independent.
Selecting Attachments
There are no rules for how to select the source or destination attachment for a joint, but one selection can be more convenient than the other. The only difference is that the interpretation of certain quantities changes if the source and destination are swapped. Some of the important quantities and the relationship with the source and destination attachments are:
•
The joint coordinate system follows the source attachment.
•
All the relative degrees of freedom are created on the destination attachment.
•
The joint moments are computed around the center of joint attached to the source attachment.
•
In the Ball Joint and Slot Joint, the inclination angle is the angle between the reference axis and the destination axis. The axial rotation occurs about the destination axis. This reference axis is defined on the source attachment.
•
In the Planar Joint, all axes in its subfeatures follow the source attachment.
Positioning the Joint Center
You can position the center of a joint in different ways:
•
At the centroid of the source attachment.
•
At the centroid of the destination attachment.
•
At the centroid of some selected entities (boundaries, edges, or points). As a special case a single point can be used.
•
Explicitly given coordinates.
Attachments must used for flexible components, and are optional for rigid components. The first two options are only available if an attachment is selected as source or destination.
Joint Axis and Local Coordinate System
The local coordinate system of a joint, which can be seen as rigidly connected to the source attachment, consists of three axes: joint axis (e1), second axis (e2), and third axis (e3). You specify the initial direction joint axis (e10), using one of the following methods:
•
Method 1: Give the components explicitly in a selected coordinate system.
•
Method 2: Select one of the axes of a selected coordinate system.
•
Method 3: Select an edge that is parallel to the joint axis.
For all methods, the axis is normalized to give a unit vector.
Constraints
Constraints are used to restrict the relative motion between the two components sharing a joint. You can specify the upper and lower bound of the relative motion. Applying constraints on the relative motion can be interpreted as placing an imaginary stopper that restricts the motion of the destination attachment with respect to the source attachment in a prescribed direction.
Theory for Joint Constraints
Locking
The Locking feature is used to lock the relative motion between the two components connected to a joint. You specify limits on the relative motion in the form of an upper and lower bound. This can be interpreted as an imaginary object (like a snap hook) that locks one of the free relative degrees of freedom of the destination attachment when it reaches the limiting value.
The Locking feature differs from Constraints in that the value of the particular joint degree of freedom becomes constant for the rest of the analysis once it attains its prescribed limiting value.
Theory for Joint Locking
Springs and Dampers on Joints
You can use the Spring and Damper feature to apply a spring or a dashpot to act on the relative motion in a joint. A dashpot can be used to account for various kinds of losses at the joint. The spring can be given a predeformation so that the spring equilibrium position is not the same as the initial state.
Theory for Springs and Dampers on Joints
Elasticity in Joints
In the directions in which relative motion is not allowed in a joint, the default case is that the source and destination attachments are rigidly connected. It is possible to instead insert an elastic connection by setting Joint Elasticity to Elastic joint in the settings for the joint. There are several occasions when you may want to use this option:
•
There is a physical flexibility in the joint, like a bushing.
•
The mechanical system is overconstrained by the chosen set of joints. You can then release some degrees of freedom by making them elastic. This should typically be done in directions where no significant forces act.
•
You have a mechanism which is not possible to model by the built-in joints. You can then add degrees of freedom to the built-in joint by making them elastic, and not supply any stiffness.
•
The joint gets deactivated and the two bodies are no longer connected after certain time in a transient simulation. You then can use the elastic joints for this purpose by making the stiffness and damping properties a function of time.
In addition to the elasticity, you can also add viscous damping to a degree of freedom selected as being elastic.
The theory for joint elasticity is described separately for each joint type:
•
Joint Elasticity in Prismatic Joint
•
Joint Elasticity in Hinge Joint
•
Joint Elasticity in Cylindrical Joint
•
Joint Elasticity in Planar Joint
•
Joint Elasticity in Ball Joint
•
Joint Elasticity in Slot Joint
•
Joint Elasticity in Reduced Slot Joint
•
Joint Elasticity in Fixed Joint
•
Joint Elasticity in Universal Joint
Prescribed Motion
With Prescribed Motion you can control the relative motion in a joint, either by prescribing the displacement or the velocity. This is useful when the degrees of freedom in the joint are not free but are a known function of time. This is common in the field of robotics, for example.
Evaluating reaction force for the prescribed motion by selecting Evaluate reaction forces in the Reaction force settings section of the settings for Prescribed Motion has several benefits over evaluating it using joint forces and moments computed using weak constraints:
•
It includes the contributions of springs, dampers, and friction applied on the joint.
•
It works even if there are redundant constraints in the system, especially in a rigid body system, since joint constraints cannot be applied in the weak form in such a system.
•
It is computationally more efficient as it adds fewer degrees of freedom.
Theory for Prescribed Motion on Joints
Applied Forces and Moments on Joints
The Applied Force and Moment feature is used to apply forces and moments on all types of joints. It can be applied at the source or destination joint attachment, or directly to the joint degrees of freedom.
Theory for Applied Forces and Moments on Joints
Friction
The Friction feature is used to add frictional loss to a joint. It is available for Prismatic Joint, Hinge Joint, Cylindrical Joint, Screw Joint, Planar Joint, and Ball Joint.
The friction force is modeled using a continuous friction law, which is capable of modeling sliding-sticking phenomena. A strict application of Coulomb’s law involves discrete transition from sticking to sliding and vice versa, as dictated by a vanishing relative velocity. These discrete transitions cause numerical difficulties and to avoid them, the friction force is approximated with a continuous friction law:
where Ff is the friction force, μ is the frictional coefficient, N is the normal force, v is the slip velocity, and v0 is the characteristic slip velocity. The term
is called the regularization factor.
The regularization factor is used to smoothen the friction force discontinuity. The characteristic slip velocity should be chosen to be small in comparison to the characteristic relative velocities encountered during the simulation. The continuous friction law describes both sliding and sticking behavior, that is, it completely replaces Coulomb’s law. Sticking is replaced by creeping between the contacting bodies with a small relative velocity.
Theory for Friction in Joints
Computing Joint Forces and Moments
It is often of interest to evaluate the internal forces (the reaction forces) in a joint. There are three ways to compute forces and moments — Summing Reaction Forces Over the Boundaries, or Using Weak Constraints, or Using Penalty Formulation.
The joint forces and moments are evaluated in the global spatial coordinate system as well as in a joint local coordinate system. The joint forces and moments are referred to the center of joint in the current position. For the joints that have translational degrees of freedom, the center of joint should be interpreted as fixed to the source side.
When a joint connects two rigid bodies, the default is not to compute the joint forces. The reason is that it is common that rigid body systems are overconstrained, and then numerical problems can occur.
Summing Reaction Forces Over the Boundaries
This is the default method for computing the joint forces and moments for elastic objects. The computation can be done on either the source or destination attachment. The convention is that the force and moment are the ones acting on the attachment from the joint. The sign changes if you switch between using the source or destination attachment for the evaluation.
To use this method at least one of the components connected to the joint must be flexible.
Using Weak Constraints
When using weak constraints, the joint constraints are applied in a weak form, and the values of the Lagrange multipliers give the joint forces and moments. This works for both flexible and rigid components. The use of Lagrange multipliers can however have an effect on the structure of the equation system, which limits the solvers that can be used.
The sign convention in this case is that the forces and moments should be interpreted as acting on the destination attachment.
Using the weak constraint option in an overconstrained rigid body system will often lead to numerical difficulties.
Using Penalty Formulation
When using the penalty formulation, the constraints in the joint are implemented as stiff springs. You have to provide a penalty factor, which essentially is the spring constant. The penalty method will thus not fulfill the constraints exactly, but it has the advantage of making the model less sensitive to overconstraints.
Theory for Joint Forces and Moments Computation
Initial Values of Joint Degrees of Freedom
You do not need to supply separate initial values for joint degrees of freedom. They are consistently initialized from the degrees of freedom for a material model, either a displacement field in a flexible component or the ODE degrees of freedom in a rigid component.
In cases where locking and constraint conditions are present on a joint, the initial values of the joint degrees of freedom should be within the specified minimum and maximum limits.