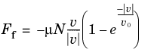The Friction feature is used to add frictional loss to a joint. It is available for
Prismatic Joint,
Hinge Joint,
Cylindrical Joint,
Screw Joint,
Planar Joint, and
Ball Joint.
where Ff is the friction force,
μ is the frictional coefficient,
N is the normal force,
v is the slip velocity, and
v0 is the characteristic slip velocity. The term
is used. Here Ff,r is the additional sliding resistance,
Ff,max is the maximum friction force, and
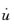
is the relative velocity in the joint. Since the joints are abstractions, there is no unique way to define the normal force
N, to which the friction force is proportional. For each joint there are several available methods for computing
N and you must select the most representative one.
where Fa are the reaction forces on the attachment boundaries, and
n is the surface normal in the deformed state.
where Fj are the joint forces,
e is the joint axis,
Mjli are the components of the joint moment in joint local coordinate system, and
αli are contribution factors given by the user.
where en0 is a direction given by the user.
Rsrc represents the rotation matrix for the rotation of the source attachment.
where p is the contact pressure, and
A is the contact area.
where Fn is the total normal force.
where 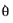
is the relative angular velocity in the joint, and
r is the hinge radius, supplied by the user.
where r is the entered cylinder radius.
where 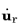
is the relative velocity vector in the joint.
where X is the material coordinates on the selected boundaries,
Xc is the center of joint, and
A is the total contact area.
where 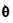
is the relative angular velocity vector at joint and
r is the ball radius. The factor
πr/ 4 is the effective ball radius.
where {ar,
br} is the relative quaternion in the joint.