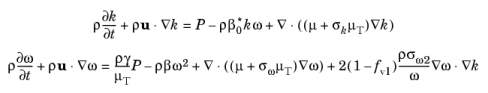To combine the superior behavior of the k-ω model in the near-wall region with the robustness of the k-ε model, Menter (Ref. 17) introduced the SST (Shear Stress Transport) model which interpolates between the two. The version of the SST model in the CFD Module includes a few well-tested (Ref. 16, Ref. 18) modifications, such as production limiters for both k and ω, the use of S instead of Ω in the limiter for μT and a sharper cut-off for the cross-diffusion term.

It is also a low Reynolds number model, that is, it does not apply wall functions. “Low Reynolds number” refers to the region close to the wall where viscous effects dominate. The model equations are formulated in terms k and ω,

and Pk is given in Equation 3-78. The turbulent viscosity is given by,

where S is the characteristic magnitude of the mean velocity gradients,

The interpolation functions fv1 and fv2 are defined as,

where lw is the distance to the closest wall.

Realizability Constraints are applied to the SST model.

The wall distance variable, lw, is provided by a mathematical Wall Distance interface that is included when using the SST model. The solution to the wall distance equation is controlled using the parameter lref. The distance to objects larger than lref is represented accurately, while objects smaller than lref are effectively diminished by appearing to be farther away than they actually are. This is a desirable feature in turbulence modeling since small objects would get too large an impact on the solution if the wall distance were measured exactly.

The most convenient way to handle the wall distance variable is to solve for it in a separate study step. A Wall Distance Initialization study type is provided for this purpose and should be added before the actual Stationary or Transient study step.

When Wall Treatment is set to Automatic the same type of formulation described for the k-ω model is applied at the boundary but with β1 instead of β0. See Automatic Wall Treatment for more details.

The SST model is low-Reynolds-number model, so the equations can be integrated all the way through the boundary layer to the wall, which allows for a no slip condition to be applied to the velocity, that is u=0.

Since all velocities must disappear on the wall, so must k. Hence, k=0 on the wall.

The corresponding boundary condition for ω is

To avoid the singularity at the wall, ω is not solved for in the cells adjacent to a solid wall. Instead, its value is prescribed by Equation 3-101 (using the variable ωw, which only exists in those cells). Accurate solutions in the near-wall region require that,

where uτ is the friction velocity which is calculated from the wall shear-stress τw,

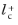
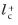
The boundary variable Distance to cell center in viscous units, lplus_cc, is available to ensure that the mesh is fine enough. According to Equation 3-102, should be about 0.5. Observe that very small values of can reduce the convergence rate.

The guidelines given in Inlet Values for the Turbulence Length Scale and Turbulent Intensity for selecting the turbulence length scale, LT, and the turbulence intensity, IT, apply also to the SST model.

The SST model was originally developed for exterior aerodynamic simulations. The recommended far-field boundary conditions (Ref. 17) can be expressed as,

where L is the approximate length of the computational domain.

The SST model has the same default initial guess as the standard k-ω model (see Initial Values) but with replaced by lref.

The default initial value for the wall distance equation (which solves for the reciprocal wall distance) is 2/lref.

The SST model applies absolute scales of the same type as the k-ω model (see Scaling for Time-Dependent Simulations).