The k-
ε model is one of the most used turbulence models for industrial applications. This module includes the standard
k-
ε model (
Ref. 1). The model introduces two additional transport equations and two dependent variables: the turbulent kinetic energy,
k, and the turbulent dissipation rate,
ε. The turbulent viscosity is modeled as
(3-76)

where Cμ is a model constant.
(3-77)
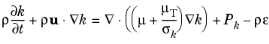
(3-78)
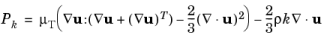
(3-79)
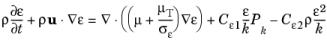
The model constants in Equation 3-76,
Equation 3-77, and
Equation 3-79 are determined from experimental data (
Ref. 1) and the values are listed in
Table 3-3.
Equation 3-77 and
Equation 3-79 cannot be implemented directly as written. There is, for example, nothing that prevents division by zero. The equations are instead implemented as suggested in
Ref. 10. The implementation includes an upper limit on the mixing length,

:
(3-80)
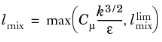
where δij is the Kronecker delta and
Sij is the strain-rate tensor. The diagonal elements of the Reynolds stress tensor must be nonnegative, but calculating
μT from
Equation 3-76 does not guarantee this. To assert that
(3-81)
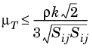
(3-82)
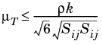
Combining equation Equation 3-81 with
Equation 3-76 and the definition of the mixing length gives a limit on the mixing length scale:
(3-83)
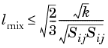
(3-84)
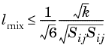
This means there are two limitations on lmix: the realizability constraint and the imposed limit via
Equation 3-80.
The k-
ε turbulence model relies on several assumptions, the most important of which is that the Reynolds number is high enough. It is also important that the turbulence is in equilibrium in boundary layers, which means that production equals dissipation. These assumptions limit the accuracy of the model because they are not always true. It does not, for example, respond correctly to flows with adverse pressure gradients and can result in under-prediction of the spatial extent of recirculation zones (
Ref. 1). Furthermore, in simulations of rotating flows, the model often shows poor agreement with experimental data (
Ref. 2). In most cases, the limited accuracy is a fair trade-off for the amount of computational resources saved compared to using more complicated turbulence models.
The flow close to a solid wall is for a turbulent flow very different from the free stream. This means that the assumptions used to derive the k-
ε model are not valid close to walls. While it is possible to modify the
k-
ε model so that it describes the flow in wall regions (see
The Low Reynolds Number k-ε Turbulence Model), this is not always desirable because of the very high resolution requirements that follow. Instead, analytical expressions are used to describe the flow near the walls. These expressions are known as wall functions.
where uτ=Cμ1/4√k is the friction velocity, is 11.06. This corresponds to the distance from the wall where the logarithmic layer meets the viscous sublayer (or to some extent would meet it if there were no buffer layer in between).
δw is limited from below so that it never becomes smaller than half the height of the boundary mesh cell. This means that
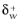
can become larger than 11.06 if the mesh is relatively coarse.
Always investigate the solution to check that δw is small compared to the dimensions of the geometry. Also check that

is 11.06 on most of the walls. If
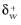
is much larger than 11.06 over a significant part of the walls, the accuracy might become compromised. Both the wall lift-off,
δw, and the wall lift-off in viscous units,
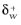
, are available as results and analysis variables.
where in turn, κv, is the von Kárman constant (default value 0.41) and
B is a constant that by default is set to 5.2.
See Ref. 10 and
Ref. 11 for further details.
The physics interfaces: Wall,
Interior Wall,
Rotating Wall, and
Rotating Interior Wall have an option to apply wall roughness by modifying the wall functions. Cebeci (
Ref. 20) suggested a model which adjusts the friction velocity for surface roughness,
(3-85)
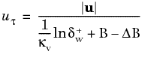
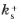
is the roughness height in viscous units,
The roughness height, ks, is the peak-to-peak value of the surface variations and the wall is relocated to their mean level.
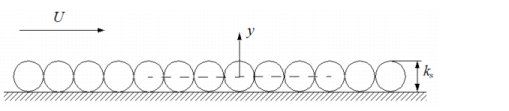
Hence, when Equation 3-85 is used the lift-off is modified according to,
where h+ is the height of the boundary mesh cell in viscous units.
Cs is a parameter that depends on the shape and distribution of the roughness elements. When the turbulence parameters
κν and
B have the values 0.41 and 5.2, respectively, and
Cs = 0.26,
ks corresponds to the
equivalent sand roughness height, kseq, as introduced by Nikuradse (
Ref. 21). A few characteristic values of the equivalent sand roughness height are given in
Table 3-4 below,
Use other values of the roughness parameter Cs and roughness height
ks to specify generic surface roughnesses.
The k-
ε equations are derived under the assumption that the flow has a high enough Reynolds number. If this assumption is not fulfilled, both
k and
ε have very small magnitudes and behave chaotically in the manner that the relative values of
k and
ε can change by large amounts due to small changes in the flow field.
(3-86)

where Uscale and
Lfact are input parameters available in the Advanced Settings section of the physics interface node. Their default values are
1 m
/s and
0.035 respectively.
lbb,min is the shortest side of the geometry bounding box.
Equation 3-86 is closely related to the expressions for
k and
ε on inlet boundaries (see
Equation 3-142).
The practical implication of Equation 3-86 is that variations in
k and
ε smaller than
kscale and
εscale respectively, are regarded as numerical noise.
