You are viewing the documentation for an older COMSOL version. The latest version is
available here.
The Direct node (

) is an attribute that handles settings for direct linear system solvers. Use it together with a
Stationary Solver,
Eigenvalue Solver, and
Time-Dependent Solver, for example. The attribute can also be used together with the
Coarse Solver attribute when using multigrid linear system solvers.
An alternative to the direct linear system solvers is given by iterative linear system solvers which are handled via the Iterative attribute node. Several attribute nodes for solving linear systems can be attached to an operation node, but only one can be active at any given time.
|
•
|
MUMPS (multifrontal massively parallel sparse direct solver) (the default).
|
|
•
|
PARDISO (parallel sparse direct solver). See Ref. 2 for more information about this solver.
|
|
•
|
SPOOLES (sparse object-oriented linear equations solver). See Ref. 3 for more information about this solver.
|
|
•
|
Dense matrix to use a dense matrix solver. The dense matrix solver stores the LU factors in a filled matrix format. It is mainly useful for boundary element (BEM) computations.
|
For MUMPS it estimates how much memory the unpivoted system requires. Enter a
Memory allocation factor to tell MUMPS how much more memory the pivoted system requires. The default is 1.2.
Select a Preordering algorithm:
Automatic (the default automatically selected by the MUMPS solver),
Approximate minimum degree,
Approximate minimum fill,
Quasi-dense approximate minimum degree,
Nested dissection, or
Distributed nested dissection.
Select the Row preordering check box (selected by default) to control whether the solver should use a maximum weight matching strategy or not. Click to clear the check box to turn off the weight matching strategy.
Select the Reuse preordering check box (selected by default) to reuse the reordering of the system, which speeds up the computation but leads to a higher memory peak.
|
|
The Reuse preordering option has a weak dependence on the system matrix. In extreme cases, this can cause the solvers to fail. If you suspect this is the problem, make sure that the Check error estimate setting is not set to No in the Error section below. Then, if the linear solvers fail and the preordering is old, a new preordering will be done.
|
The default Use pivoting is
On, which controls whether or not pivoting should be used.
|
•
|
If the default is kept (On), enter a Pivot threshold number between 0 and 1. The default is 0.01. This means that in any given column, the algorithm accepts an entry as a pivot element if its absolute value is greater than or equal to the specified pivot threshold times the largest absolute value in the column.
|
|
•
|
For Off, enter a value for the Pivoting perturbation, which controls the minimum size of pivots (the pivot threshold). The default is 10 −8.
|
Select the Block low rank factorization check box to make a low rank approximation of the LU factors, both when computing them and when storing them. The value for the
Block low rank factorization tolerance controls the quality of the approximation. The block low rank factorization is an approximate but accurate LU-factorization method that can provide a faster factorization and potentially save memory in your models. For the compression, select a type from the
Compression type list:
Normal (the default) or
Aggressive. The aggressive compression can potentially use less memory and be faster, at the expense of a slightly lower accuracy for the approximations of the LU factors.
From the Out-of-core list, choose
On to store all matrix factorizations (LU factors) as blocks on disk rather than in the computer’s memory. The solver reads some of the blocks into memory and performs the LU-factorization on the part that is currently in memory. The blocks of data are then written back to disc and new blocks are read into memory. The size of the blocks that the solver reads from disc is controlled by the in-core memory setting. Choose
Off to not store the matrix factorizations on disk. The default setting is
Automatic, which switches the storage to disk (out-of-core) if the estimated memory (for the LU factors) is exhausting the physically available memory. For the automatic option, you can specify the fraction of the physically available memory that will be used before switching to out-of-core storage in the
Memory fraction for out-of-core (a value between 0 an 1). The default is 0.99; that is, the switch occurs when 99% of the physically available memory is used.
When the Out-of-core list is set to
Automatic or
On, you can choose to specify how to compute the in-core memory to control the maximum amount of internal memory allowed for the blocks (stored in RAM and not on disk) using the
In-core memory method list:
|
•
|
Choose Automatic (the default) to derive the in-core memory from system data and a given formula:
|
(20-34)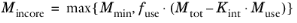
where you can specify Mmin in the
Minimum in-core memory (MB) field (default 512 MB),
fuse in the
Used fraction of total memory field (default: 0.8; that is, 80% of currently available memory), and
Kint in the
Internal memory usage factor field (default: 3).
Mtot is the total physical memory on the computer, and
Muse is the physical memory used on the computer before the solver starts.
|
•
|
Choose Manual to specify the in-core memory directly in the In-core memory (MB) field. The default is 512 MB.
|
Select a Preordering algorithm:
Nested dissection multithreaded (the default to perform the nested dissection faster when COMSOL Multiphysics runs multithreaded),
Minimum degree, or
Nested dissection.
Select a Scheduling method to use when factorizing the matrix:
|
•
|
Auto (the default): Selects one of the two algorithms based on the type of matrix.
|
|
•
|
Two-level: Choose this when you have many cores as it is usually faster.
|
Select the Row preordering check box (selected by default) to control whether the solver should use a maximum weight matching strategy or not. Click to clear the check box to turn off the weight matching strategy.
Select the Reuse preordering check box (selected by default) to reuse the reordering of the system, which speeds up the computation but leads to a higher memory peak.
|
|
The Reuse preordering option has a weak dependence on the system matrix. In extreme cases, this can cause the solvers to fail. If you suspect this is the problem, make sure that the Check error estimate setting is not set to No in the Error section below. Then, if the linear solvers fail and the preordering is old, a new preordering will be done.
|
By default, the Bunch-Kaufman pivoting check box is not selected. Click to select it and control whether to use 2-by-2 Bunch-Kaufman partial pivoting instead of 1-by-1 diagonal pivoting.
By default, the Multithreaded forward and backward solve check box is selected so that the backward and forward solves run multithreaded. This mainly improves performance when there are many cores and the problem is solved several times, such as in eigenvalue computations and iterative methods. Click to clear this check box and not run the solver multithreaded.
The Pivoting perturbation field controls the minimum size of pivots (the pivot threshold
ε).
Select the Parallel Direct Sparse Solver for Clusters check box to use the Parallel Direct Sparse Solver (PARDISO) for Clusters from the Intel
® MKL (Intel
® Math Kernel Library) when running COMSOL Multiphysics in a distributed mode.
From the Out-of-core list, choose
On to store all matrix factorizations (LU factors) as blocks on disk rather than in the computer’s memory. The solver reads some of the blocks into memory and performs the LU-factorization on the part that is currently in memory. The blocks of data are then written back to disc and new blocks are read into memory. The size of the blocks that the solver reads from disc is controlled by the in-core memory setting. Choose
Off to not store the matrix factorizations on disk. The default setting is
Automatic, which switches the storage to disk (out-of-core) if the estimated memory (for the LU factors) is exhausting the physically available memory. For the automatic option, you can specify the fraction to be stored on disk in the
Memory fraction for out-of-core (a value between 0 an 1; the default is 0.99). If needed, the out-of-core PARDISO solver automatically increases the in-core memory that is required.
When the Out-of-core list is set to
Automatic or
On, you can choose to specify how to compute the in-core memory to control the maximum amount of internal memory allowed for the blocks (stored in RAM and not on disk) using the
In-core memory method list:
|
•
|
Choose Automatic (the default) to derive the in-core memory from system data and a given formula:
|
(20-35)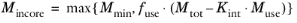
where you can specify Mmin in the
Minimum in-core memory (MB) field (default 512 MB),
fuse in the
Used fraction of total memory field (default: 0.8; that is, 80% of currently available memory), and
Kint in the
Internal memory usage factor field (default: 3).
Mtot is the total physical memory on the computer, and
Muse is the physical memory used on the computer before the solver starts.
|
•
|
Choose Manual to specify the in-core memory directly in the In-core memory (MB) field. The default is 512 MB.
|
Select a Preordering algorithm:
Best of ND and MS (the best of nested dissection and multisection),
Minimum degree,
Multisection, or
Nested dissection.
Enter a Pivot threshold number between 0 and 1. The default is 0.1. This means that in any given column the algorithm accepts an entry as a pivot element if its absolute value is greater than or equal to the specified pivot threshold times the largest absolute value in the column.
|
•
|
The default is Automatic, meaning that the main solver is responsible for error management. The solver checks for errors for every linear system that is solved. To avoid false termination, the main solver continues iterating until the error check passes or until the step size is smaller than about 2.2·10 −14. With this setting, linear solver errors are either added to the error description if the nonlinear solver does not converge, or added as a warning if the errors persist for the converged solution.
|
|
•
|
Choose Yes to check for errors for every linear system that is solved. If an error occurs in the main solver, warnings originating from the error checking in the direct solver appear. The error check asserts that the relative error times a constant ρ is sufficiently small. This setting is useful for debugging problems with singular or near singular formulations.
|
|
•
|
Choose No for no error checking.
|
Use the Factor in error estimate field to manually set the constant
ρ. The default is 1. See
Convergence Criteria for Linear Solvers for more information.
The Iterative refinement check box is selected by default (except for the eigenvalue solver) so that iterative refinement is used for direct and iterative linear solvers. For linear problems (or when a nonlinear solver is not used), this means that iterative refinement is performed when the computed solution is not good enough (that is, the error check returned an error). It is possible that the refined solution is better. Iterative refinement can be a remedy for instability when solving linear systems with a solver where convergence is slow and errors might be too large, due to ill-conditioned system matrices, for example. If a nonlinear solver is used, iterative refinement is not used by default. You can often get away with intermediate linear solver steps, but if that is not the case, select the
Use in nonlinear solver check box to use an iterative refinement. The default value in the
Maximum number of refinement field is 15; you can change it if needed. By default, the
Error ratio bound is set to 0.5. For both linear and nonlinear solver runs where iterative refinements are used, iterative refinements should be terminated when the error is not decreasing along the iteration. Therefore, the error ratio bound should always be smaller than 1. Because the error is computed in the
L2 norm, the error ratio bound should always be greater than 0. Setting the error ratio bound to 0.5, as suggested by
Ref. 9, is a more cautious approach that rarely yields significant underestimations or overestimations of errors, and it always terminates quickly compared to an error ratio bound much closer to 1. When
Check error estimate is set to
Automatic, a single warning,
Iterative refinement triggered, appears in the
Log window if the iterative refinement is triggered. When
Check error estimate is set to
Yes, the same warning and the number of iterative refinements applied in each linear solver call are shown in the
Log window.