Choosing the Right Linear System Solver
The following pertains to the Direct attribute node. All linear system solvers above work on general sparse linear systems of the form Ax = b and use LU factorization on the matrix A to compute the solution x. In doing so, they use a preordering algorithm that permutes the columns of A to minimize the number of nonzeros in the L and U factors. Popular preordering algorithms include Minimum degree, Nested dissection, and Multisection. All solvers run distributed when running COMSOL Multiphysics in distributed mode (on clusters, for example). All linear system solvers benefit from shared memory parallelism (multicore processors, for example). MUMPS and PARDISO have an option for reusing the preordering, which speeds up the computation but leads to a higher memory peak.
This section reviews Linear System Solver Selection Guidelines, Which Models Are Positive Definite?, and Elliptic and Parabolic Models.
Linear in the COMSOL Multiphysics Programming Reference Manual.
The MUMPS Solver
The MUMPS solver works on general systems of the form Ax = b and uses several preordering algorithms to permute the columns and thereby minimize the fill-in. MUMPS is multithreaded on platforms that support multithreading and also supports solving on distributed memory architectures through the use of MPI. The code is written in Fortran 90. For further details about MUMPS, see Ref. 1.
The PARDISO Solver
The PARDISO solver works on general systems of the form Ax = b. In order to improve sequential and parallel sparse numerical factorization performance, the solver algorithms are based on a Level-3 BLAS update, and they exploit pipelining parallelism with a combination of left-looking and right-looking supernode techniques. PARDISO is multithreaded on platforms that support multithreading. On distributed memory architectures, if you clear the Parallel Direct Sparse Solver for Clusters check box or if you run PARDISO in the out-of-core mode, the solver settings are changed to corresponding MUMPS settings. The code is written in C and Fortran. COMSOL Multiphysics uses the PARDISO version developed by Olaf Schenk and collaborators (Ref. 2), which is included with Intel® MKL (Intel Math Kernel Libraries).
The SPOOLES Solver
The SPOOLES solver works on general systems of the form Ax = b using the multifrontal method and direct LU factorization of the sparse matrix A. When the matrix A is symmetric or Hermitian, the solver uses an LDLT version of the algorithm, which saves half the memory. SPOOLES uses several preordering algorithms to permute the columns and thereby minimize fill-in. SPOOLES is multithreaded on platforms that support multithreading and also supports solving on distributed memory architectures through the use of MPI. The code is written in C. COMSOL uses SPOOLES version 2.2 developed by Cleve Ashcraft and collaborators (Ref. 3).
The Dense Matrix Solver
The dense matrix solver works on general systems of the form Ax = b. The dense matrix solver uses LAPACK (Ref. 4) for multithreaded solves and ScaLAPACK (Ref. 5) for distributed memory architectures. This solver is mainly useful for cases where the system matrices are densely populated, such as boundary element (BEM) models.
Linear System Solver Selection Guidelines
The physics interface in the model selects a default linear system solver that usually is appropriate for the problem type, at least for single-physics interface models. If the default solver does not perform well, use the following guidelines to choose a linear system solver.
1
Try the PARDISO direct solver.
2
Try the MUMPS direct solver.
3
If the solver still runs out of memory or is too slow, use one of the iterative solvers GMRES, FGMRES, BiCGStab, or TFQMR. Select a preconditioner according to the guidelines in the section about the iterative solver.
4
If the system is positive definite and real symmetric or Hermitian, try the conjugate gradients iterative solver, which is more memory-efficient and sometimes faster than GMRES, FGMRES, BiCGStab, and TFQMR. Select a symmetric preconditioner. Alternatively, try the SPOOLES direct solver. It often uses less memory but is less numerically stable. SPOOLES is also slower.
Which Models Are Positive Definite?
A model with a real symmetric or Hermitian system matrix is often also positive definite, which means that a number of efficient linear system solvers are applicable. Further, the simple preconditioners SSOR, SOR, SORU, Jacobi (diagonal scaling), and the multigrid solvers benefit from a positive definite matrix. A real symmetric or Hermitian matrix is positive definite if all its eigenvalues are positive.
For stationary problems, the system matrix is the Jacobian (stiffness) matrix A. This means that stationary models in diffusion, electromagnetics, heat transfer by conduction, and structural mechanics usually have a positive definite system matrix.
For time-dependent problems, the system matrix is of the form A + σB + σ2C, where B is the damping matrix, C is the mass matrix, and σ > 0 is inversely proportional to the time step (if C = 0, then B is often called the mass matrix). Because these matrices are often positive definite, time-dependent models in diffusion, electromagnetics, structural mechanics, and heat transfer by conduction usually have a positive definite system matrix.
For eigenvalue problems, the system matrix is of the form A − σB + σ2C, where σ is the shift — that is, the number around which the software searches for eigenvalues (specified in the Search for eigenvalues around field; the default is 0). Because A, B, and C are usually positive definite, eigenvalue problems in acoustics, diffusion, electromagnetics, heat transfer by conduction, and structural mechanics usually have a positive definite system matrix if σ ≤ 0. 
Elliptic and Parabolic Models
The classes of elliptic and parabolic models include the positive definite models. For such models, the efficient multigrid preconditioners often perform well. A simplified definition of these classes reads as follows. A system of stationary or eigenvalue second-order PDEs is elliptic if the second-order terms in the PDE give rise to a positive definite Jacobian matrix. 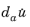A system of time-dependent PDEs has a time derivative term of the form , where the mass coefficient da is often a positive definite matrix and the ea coefficient is 0. Such a system is parabolic if the second-order terms in the PDE give rise to a positive definite Jacobian matrix.
Stationary or eigenvalue models in acoustics, convection-diffusion, electromagnetics, heat transfer, and structural mechanics are usually elliptic. Likewise, time-dependent models in convection-diffusion, electromagnetics, and heat transfer are often parabolic. The Navier–Stokes equations, wave-type equations, or formulations involving weak constraints are neither elliptic nor parabolic.