You are viewing the documentation for an older COMSOL version. The latest version is
available here.
Use the Eigenvalue Solver (

) to find the solution to linear or linearized eigenvalue problems (also called eigenfrequency problems). This solver is automatically used when an
Eigenvalue or
Eigenfrequency study is added to the model.
Use the Defined by study step list to specify if the settings are synchronized with the corresponding study step. Select
User defined to specify the properties below (in addition to the relative tolerance, which is always available).
The settings here are similar to those for the Eigenvalue study step, with the following exceptions:
From the Eigenvalue transformation list, select a transformation method for transforming the eigenvalues into another related quantity. The default is
None, which keeps the original eigenvalues. Depending on the physics in the model, other transformations might also be available.
The number in the Relative tolerance field (default 1.0·10
−6) controls the relative error in the computed eigenvalues.
Select the Enter transformed values check box to enter the values to search around as the transformed value (an eigenfrequency, for example) instead of the corresponding eigenvalue.
The default setting for the Integration type for estimation list and the
Number of integration points for estimation list is
Automatic. When you choose
Automatic in the
Integration type for estimation list, it uses the Gauss type for real symmetric or Hermitian eigenvalue solvers and the trapezoidal method for other types of solver. Otherwise, choose
Gauss or
Trapezoidal to use only one of those method. When you choose
Automatic in
Number of integration points for estimation, it is 6 for real symmetric or Hermitian eigenvalue solvers and 16 for other types of solvers.
Select the Distribute linear system solution check box to run the FEAST eigenvalue solver in parallel. See
Running FEAST in a Parallel MPI Mode for more information.
When you have selected A posteriori residual check, the solver a posteriori explicitly computes the relative residual of the eigenpair and checks that this quantity is smaller that 100*
tol, where
tol is the
Relative tolerance. Notice that, in order to do this computation, the solver needs to store the
K,
D, and
E matrices, and therefore, this option requires more memory. If any residual is larger than the tolerance, a
Warning node appears with information about which eigenpairs it concerns. That information also appears in the solver log.
From the Compute and store left eigenvectors list, choose
Automatic (the default),
On, or
Off. The
Automatic option typically is the same as
Off, but, depending on the other settings, if needed, the left eigenvector will be computed (and eventually stored). The eigenvectors referred to as just “eigenvectors” are right eigenvectors. A left eigenvector is defined as a row vector
XL that satisfy
XL A = λLXL . For example, for sensitivity and optimization, when the matrices are nonsymmetric, left eigenvectors will be computed. Also, left eigenvectors can be used for projecting equations in the modal solver.
If the eigenvalue itself appears nonlinearly, the solver reduces the problem to a quadratic approximation around an eigenvalue linearization point. Select the Transform eigenvalue linearization point check box to transform the linearization point value using the selected eigenvalue transformation. Specify the value of the linearization point in the
Value of eigenvalue linearization point field (SI unit: rad/s).
For other settings, see the Eigenvalue or
Eigenfrequency study settings. When the eigenvalue search settings are defined by the study step, the settings above that correspond to similar study settings are not available.
This section is only visible when the study contains a Stationary Then Eigenfrequency study step. It can be used to specify which dependent variables are computed with the Eigenvalue solver. The same dependent variable cannot appear in the equivalent section of the
Stationary Solver, control variables excepted.
From the Linearity list, choose
Linear (the default) or
Linear perturbation.
|
•
|
Initial expression (the default) to use the expressions specified on the Initial Values nodes under a specific physics interface as a linearization point.
|
|
•
|
Solution to use a solution as linearization point.
|
Use the Solution list to specify which solution to use if
Prescribed by is set to
Solution:
|
•
|
Select Zero (the default) to use a linearization point that is identically equal to zero.
|
Select the Store linearization point and deviation in output check box to store the linearization point and the deviation from that linearization instead of the total solution.
Select an option from the Scaling of eigenvectors list to specify the scaling method used to normalize the eigenvectors. Select:
|
•
|
RMS to use root mean square normalization. This RMS scaling of the eigenvector u is such that 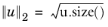 .
|
|
•
|
Maximum to use maximum norm normalization. The degree of freedom with the largest absolute value will be assigned the value specified in the Maximum absolute value field (default: 1), so that 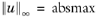 . You can change the maximum absolute value to, for example, keep the eigenmodes small in value. The physics interfaces for structural mechanics set this value to a small number during the solver generation.
|
|
•
|
Mass matrix to scale the eigenvectors such that the modal masses become unity.
|
The eigenvalue solver is an iterative algorithm. Use the Maximum number of eigenvalue iterations field to limit the number of iterations (default: 300).
When you use the ARPACK solver, you can use the Dimension of Krylov space field to control the algorithm’s memory use. The default value of 0 means that the solver sets the dimension automatically to approximately twice the number specified in the
Desired number of eigenvalues field in the
General section.
Click the Add button (

) to add a constant and then define its name in the
Constant name column and its value (a numerical value or parameter expression) in the
Constant value column. By default, any defined parameters are first added as the constant names, but you can change the names to define other constants. Click
Delete (

) to remove the selected constant from the list.
The Log section contains logs of the eigenvalue solver results and properties of the assembled system, including the solver iterations and the total solution time. This log is stored in the Model MPH-file.
|
|
Conical Quantum Dot: Application Library path COMSOL_Multiphysics/Equation_Based/conical_quantum_dot
|