You are viewing the documentation for an older COMSOL version. The latest version is
available here.
In The Semiconductor Equations section, a closed-form expression was computed for the electron and hole mobilities by making the relaxation-time approximation and by assuming a particular form for the scattering time as a function of energy. Any mechanism that disturbs the perfect periodicity of the lattice can produce scattering of the carriers. Such mechanisms include:
(3-79)

where μE, the mobility including high field effects, is a function of
μs (the surface mobility), which in turn is a function of the mobility model for phonon (or lattice) and impurity scattering (
μLI).
COMSOL Multiphysics uses a general mechanism to combine both user-defined and predefined mobility models that accommodate combinations of the form given in
Equation 3-79. Mobility models are added as subnodes to the
Semiconductor Material Model node. If the mobility model requires an input mobility, this is selected from the available mobilities appropriate for this model (individual selections are required for both the electron and hole mobility inputs). Multiple user-defined mobility models can be added and these can be used as inputs to predefined or other user-defined mobility models. The user-defined mobility models are always available as inputs in predefined mobility models (if the model requires an input). Within this system it is possible to mix user-defined mobility models with models predefined by COMSOL Multiphysics in a very general manner. The model used within the simulation is selected for electrons and holes by changing the electron mobility and the hole mobility settings in the Mobility Model section of the Semiconductor Material Model node, which by default uses a constant mobility obtained from the material properties.
The Power Law Mobility Model (L) is a simple mobility model and requires no input as it includes scattering due to phonons. The electron (
μn,pl) and hole (
μp,pl) mobilities are determined by the equations:
where T is the lattice temperature and
μp,pl,
μp,pl,
αn,
αp, and
Tref are material properties. For silicon the values of the material properties are taken from
Ref. 16.
The empirical Arora Mobility Model (LI) includes both phonon and impurity scattering. The electron (
μn,ar) and hole (
μp,ar) mobilities are determined by the equations:
where T is the lattice temperature,
Na− is the ionized acceptor concentration, and
Nd+ is the ionized donor concentration. All the other parameters are material properties. For silicon the values of the material properties are taken from
Ref. 16.
The Klaassen Unified Mobility Model (LIC) (sometimes referred to as Philips Unified Mobility Model) includes the combined effects of lattice (phonon) scattering (indicated by the ‘L’ in the parenthesis), impurity scattering (‘I’ in the parenthesis), and carrier-carrier scattering (‘C’ in the parenthesis). Screening of the impurities by the charge carriers and clustering of impurities at high doping levels are also taken into account. The Klaassen unified mobility model involves many parameters. The set of equations defining the model is shown in the
Equation section in the graphical user interface. This mobility model is based on
Ref. 17 and
Ref. 18.
The Fletcher Mobility Model (C) adds carrier-carrier scattering to an existing mobility model (or to a constant input mobility). It accepts input mobilities of type L or LI, as well as user-defined input mobilities.
where T is the lattice temperature,
μin,n and
μin,p are the electron and hole input mobilities,
n is the electron concentration, and
p is the hole concentration.
F1 (SI unit: s
2A/(m
3kg)),
F2 (SI unit: 1/m
2), and
Tref are material properties. For silicon the values of the material properties are taken from
Ref. 20.
The Lombardi Surface Mobility Model (S) adds surface scattering resulting from surface acoustic phonons and from surface roughness. Mobility contributions corresponding to these effects are combined with the input mobility using Matthiessen’s rule. The model accepts input mobilities of type L, LI, or C as well as user defined input mobilities. The model is based on
Ref. 21. The electron (
μn,lo) and hole (
μp,lo) mobilities are determined by the following equations:
where T is the lattice temperature,
μin,n and
μin,p are the electron and hole input mobilities,
Na- is the ionized acceptor concentration,
Nd+ is the ionized donor concentration,
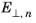
is the component of the electric field perpendicular to the electron current and
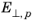
is the component of the electric field perpendicular to the hole current. All other parameters in the model are material properties (note that
δn and
δp have units of V/s). The material properties for silicon are also obtained from this reference
Ref. 21.
The Caughey-Thomas Mobility Model (E) adds high field velocity scattering to an existing mobility model (or to a constant input mobility). It accepts input mobilities of type L, LI, C, or S as well as user defined input mobilities. The model is based on
Ref. 22. The electron (
μn,lo) and hole (
μp,lo) mobilities are determined by the following equations:
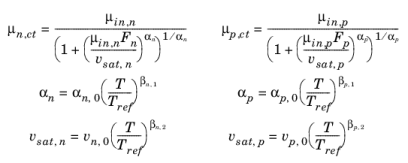
where T is the lattice temperature,
μin,n and
μin,p are the electron and hole input mobilities and
Fn and
Fp are the driving forces for electrons and holes (currently there are a few options for the driving forces selectable from a list, the default is
Fn=
E||,n and
Fp=E||,p where
E||,n is the magnitude of the component of the electric field parallel to the electron current and
E||,p is the magnitude of the component of the electric field parallel to the electron current). All other parameters in the model are material properties (note that
vn,0 and
vp,0 are the saturation velocities for electrons and holes and have units of m/s). The material properties for silicon are also obtained from
Ref. 22.
The User-Defined Mobility Model can be used to create electron and hole mobilities with user-defined expressions for the electron and hole mobilities. These mobility models can be combined with other user-defined or predefined mobility models in arbitrary combinations. These mobility models can take other defined mobilities as inputs. By default the output mobility is set to the input mobility for both electrons and holes. However, it is possible to change the expression for the output mobility so that it is any function of the input mobility (or indeed a function that does not depend on the input mobility). The default value is set in this way to make it straightforward to access the variable in which the input mobility is stored.