The Spalart-Allmaras turbulence model is a one-equation turbulence model designed mainly for aerodynamic applications. It is a low Reynolds number model, that is, it does not utilize wall functions. “Low Reynolds number” refers to the region close to the wall where viscous effects dominate.

The model gives satisfactory results for many engineering applications, in particular for airfoil and turbine blade applications for which it is calibrated. It is however not appropriate for applications involving jet-like free shear regions. It also has some nonphysical properties. For example, it predicts zero decay rate for the eddy viscosity in a uniform free-stream (Ref. 1).

Compared to the low Reynolds number k-ε model, the Spalart-Allmaras model is generally considered more robust and is often used as a way to obtain an initial solution for more advanced models. It can give reasonable results on relatively coarse meshes for which the low Reynolds number k-ε model does not converge or even diverges.

This module includes the standard version of the Spalart-Allmaras model without the trip term (see Ref. 1 and Ref. 14). The model solves for the undamped turbulent kinematic viscosity, :

are the mean strain rate and mean rotation rate tensors, lw, is the distance to the closest wall and ν=μ/ρ is the kinematic viscosity. The turbulent viscosity is calculated by

The implementation of the production term includes the rotation correction suggested in Ref. 14. See also Ref. 15. The terms r and are furthermore regularized according to Ref. 14.

Pseudo Time Stepping for Turbulent Flow Models is by default applied to the stationary form of the Spalart-Allmaras model.

For the Spalart-Allmaras turbulence model, the following relation is valid from the wall all the way through the log layer (Ref. 24):

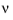
δw+ from Equation 3-127 can be used in Equation 3-92 to calculate uτlog which in turn gives uτ through Equation 3-94. With uτ, the boundary condition for is given by .

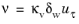
These relations are applied to the lift-off concept shown in Figure 3-9 which gives δw = hw/2. The boundary conditions for the momentum equations are a no-penetration condition, u·n = 0 and the traction condition given by Equation 3-95.

The resulting wall resolution, δw+, is available as the postprocessing variable. Delta_wPlus.

The Spalart-Allmaras model is consistent with a no slip boundary condition, that is u=0. Since, there can be no fluctuations on the wall, the boundary condition for is .

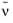
The Spalart-Allmaras model can be considered to be well resolved at a wall if is of order unity. is the distance, measured in viscous units, from the wall to the center of the wall adjacent cell and can be evaluated as the boundary variable: Distance to cell center in viscous units, lplus_cc. See also Wall for boundary condition details.

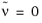
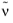
The Spalart-Allmaras model applies absolute scales of the same type as the k-ε model (see Scaling for Time-Dependent Simulations) except that the scale for is given directly by the νscale parameter available in the advanced section of the physics interface node. The default value for νscale is 5·10−6 m2/s.