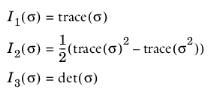As defined above J2 ≥ 0. In many material models, the most relevant invariants are I1, J2, and J3. I1 represents the effect of mean stress, J2 represents the magnitude of shear stress, and J3 contains information about the direction of the shear stress.

This ordering is true also for the 2D cases. The corresponding principal directions vpi are orthonormal.

The principal stresses are the roots of the characteristic equation (Cayley–Hamilton theorem)

The expressions described in Equation 3-10 and Equation 3-11 enter into expressions that define various kind of yield and failure surfaces. A yield surface is a surface in the 3D space of principal stresses that circumscribe an elastic state of stress.

It is possible to define other variables in terms of the principal invariants. One common auxiliary variable is the Lode angle θ.

The Lode angle is bounded to 0 ≤ θ ≤ π/3 when the principal stresses are sorted as σp1 ≥ σp2 ≥ σp3 (Ref. 54). Following this convention, θ = 0 corresponds to the tensile meridian, and θ = π/3 corresponds to the compressive meridian.

The principal stresses (σp1, σp2, and σp3) are then written in terms of the invariants I1, J2, and the Lode angle θ as

The octahedral plane (also called π-plane or deviatoric plane) lies perpendicular to the hydrostatic axis in the Haigh–Westergaard Coordinates. The stress normal to this plane is σoct =  I1/3, also called mean stress or hydrostatic stress, and the shear stress on that plane is defined by .

The profile of the yield surface on the octahedral plane is useful for visualizing changes in yield limits under compression or tension, and it illustrates how the criterion depends on the Lode angle. See for instance the Tresca Criterion and the Mohr–Coulomb Criterion.

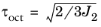
The profile of the yield function on the Octahedral Plane is useful for denoting changes in the yield limit under different loading conditions, for example, different yield limits in compression or tension. For Porous Plasticity, COMSOL Multiphysics provides three alternative definitions of the function Γ(θ) that controls the shape of the yield function in the octahedral plane:

Gudehus (Ref. 99) proposed an octahedral section that changes with the Lode angle θ. The change in the cross-sectional shape depends on one parameter as

A value of c = 1 represents a circular section. Independently of the value of the parameter c, the function equals Γ(0) = 1 at the tensile meridian (θ = 0), and Γ(π / 3) = 1 / c at the compressive meridian. For c < 1, the tensile strength is lower than the compressive strength. The function Γ(θ) is thus an approximation of the ratio of tensile to compressive strength. For the function to be convex, the parameter c has a lower bound of 7/9 and an upper bound of 9/7.

Panteghini and Lagioia (Ref. 100) proposed a three-parameter function to control the octahedral section based on the Lode angle:

The function Γ(θ) was derived with the purpose to recover common soil plasticity criteria, including a rounded Mohr–Coulomb Criterion, the Matsuoka–Nakai Criterion, and the Lade–Duncan Criterion. However, the three parameters provide a flexible option to control the octahedral section in a general manner. Setting the parameter c2 < 1 creates a continuous and C2 differentiable function.

For Elastoplastic Soils, COMSOL Multiphysics provides three alternative definitions for the function Γ(θ):

The meridional plane, also called Rendulic plane, is the profile of the yield criterion at a given Lode angle, typically at the compressive meridian θ = π/3.

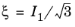
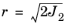
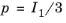
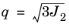
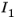
In the Haigh–Westergaard Coordinates, the meridional plane is given by the coordinates and , but it also common to visualize criteria in the pq-plane, given by the coordinates and , or the plane given by the axes and .
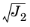