A key concept for porous plasticity models is the evolution of the relative density, which is the solid volume fraction in a porous material. The relative density is related to the porosity (or void volume fraction)
ϕ by
Shima and Oyane (Ref. 101) proposed a yield surface for modeling the compaction of porous metallic structures fabricated by sintering. The criterion can be applied for powder compaction at both low and high temperatures.
The yield function and associated plastic potential in the original Shima–Oyane criterion is defined by an ellipsoid in the stress space. The plastic potential Qp is written in terms of both von Mises equivalent stress and mean pressure, and it also considers isotropic hardening due to changes in porosity. The plastic potential is defined by
(3-78)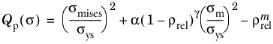
where σmises is the equivalent (von Mises) stress,
σys is the yield stress,
σm is the mean stress, and
ρrel is the relative density. The material parameters
α,
γ, and
m are obtained from curve fitting experimental data. Typical material parameter values for copper aggregates are
α =
6.2,
γ =
1.03, and
m =
5.
The shape of the yield function in the Octahedral Plane can be made a function of the
Lode angle θ by using any of the functions described in
Octahedral Section.
Here, Γ(
θ) is a function that defines the shape of the yield function in the
Octahedral Plane.
The most common choice, Γ(
θ) = 1, results in a circular section that recovers the original Shima–Oyane criterion.
The Gurson criterion (Ref. 102) consists in a pressure-dependent yield function to describe the constitutive response of porous metals. The yield function is derived from the analytical expression of an isolated void immersed in a continuum medium. The void volume fraction, or porosity
ϕ, is chosen as main variable.
(3-79)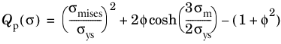
here, σmises is the equivalent (von Mises) stress,
σys is the yield stress,
σm is the mean stress, and
ϕ is the porosity.
The shape of the yield function in the Octahedral Plane can be made a function of the
Lode angle θ by using any of the functions described in
Octahedral Section.
Here, Γ(
θ) is a function that defines the shape of the yield function in the
Octahedral Plane. The most common choice,
Γ(
θ) = 1, results in a circular section that recovers the original criterion.
Tvergaard and Needleman modified the Gurson Criterion for porous plasticity to include parameters to better fit experimental data (
Ref. 103-
104). The resulting criterion is called the Gurson–Tvergaard–Needleman (GTN) criterion in the literature. The plastic potential for the GTN criterion reads
(3-80)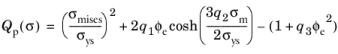
here, σmises is the equivalent stress,
σys is the yield stress,
σm is the mean stress, and
ϕe is the effective void volume fraction (effective porosity). Typical correction parameter values are
q1 =
1.5,
q2 =
1.03, and
q3 =
q12.
The shape of the yield function in the Octahedral Plane can be made a function of the
Lode angle θ by using any of the functions described in
Octahedral Section.
Here, Γ(
θ) is a function that defines the shape of the yield function in the
Octahedral Plane. The most common choice,
Γ(
θ) = 1, results in a circular section that recovers the original criterion.
The effective void value fraction (or effective porosity) ϕe used in the plastic potential is a function of the current porosity
ϕ and other material parameters. It is often given by a bilinear function
where ϕc is the critical void volume fraction (critical porosity) at which void coalescence begins, and
ϕf is the void volume fraction at failure.
When the porosity increases up to the value of failure, ϕf, the effective porosity takes a maximum value of
ϕm and the porous material loses the capacity to carry stresses. The maximum porosity value is derived from other parameters
Since typical values for the parameters are q3 =
q12, the maximum porosity value is given by
ϕm = 1/q1.
A similar definition for ϕe that gives a smooth response as the material reaches failure is suggested in
Ref. 106. It is based on a modification such that the effective void volume fraction reaches its maximum value asymptotically
The Fleck–Kuhn–McMeeking (FKM) criterion (Ref. 107), was developed to model the plastic yielding of metal aggregates of high porosity. The yield function and associated plastic potential is derived for randomly distributed particles. The criterion is considered relevant for aggregates with porosity between 10% and 35%. The plastic potential for the FKM criterion reads
(3-81)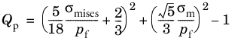
here, σmises is the equivalent (von Mises) stress and
σm is the mean stress. The
flow strength of the material under hydrostatic loading,
pf, is computed from
here, σys is the yield stress, and
ϕ is the void volume fraction (porosity). The maximum void volume fraction
ϕm typically takes the value of 36%, the limit of dense random packing of sintered powder.
The shape of the yield function in the Octahedral Plane can be made a function of the
Lode angle θ by using any of the functions described in
Octahedral Section.
Here, Γ(
θ) is a function that defines the shape of the yield function in the
Octahedral Plane. The most common choice,
Γ(
θ) = 1, results in a circular section that recovers the original criterion.
The yield function of the original FKM criterion (Ref. 107) is discontinuous at
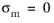
. In COMSOL Multiphysics the discontinuity in the plastic potential is resolved as described in
Apex Smoothing.
The FKM–GTN criterion is a combination of the Fleck–Kuhn–McMeeking Criterion (FKM) and the
Gurson–Tvergaard–Needleman Criterion (GTN), intended to cover a wider range of porosities (
Ref. 108–
109). The GTN model is used for low void volume fractions (porosity lower than 10%), and for void volume fractions higher than 25%, the FKM criterion is used. In the transition zone, a linear combination of both criteria is used. The plastic potential can be associated, or follow either the GTN or FKM potential.
Since the relative density is related to the porosity ϕ by
ρrel =
1 − ϕ, the change in porosity is also controlled by the change in plastic volumetric strain
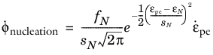 for
for 
here, εN is the mean strain for nucleation,
fN is the void volume fraction for nucleating particles, and
sN is the standard deviation. Typical values for these parameters are
εN =
0.04,
sN =
0.1, and
fN =
0.04. It is assumed that nucleation appears only in tension, and that there is no nucleation in compression.
here, kw is a material parameter,
ϕ is the current porosity,
nD is a deviatoric tensor coaxial to the stress tensor, and
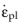
is the plastic strain rate, which depends on the porous plasticity model. The weight
w is computed from the
Invariants of the Stress Tensor as
where θ is the
Lode angle.
The variable w has a value of
w =
0 at the compressive and tensile meridians (
θ =
0 and
θ =
π/3), and it attains its maximum value,
w =
1, for
θ =
π/6, which corresponds to maximum shear.
depends on the initial yield stress σys0, the hardening function
σh, and the equivalent plastic strain in the porous matrix
εpe.
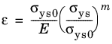 for
for 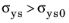
where σys0 is the initial yield stress,
m is the stress hardening exponent, and
E is the Young’s modulus.
By writing the onset of plasticity as ε0 =
σys0/E, and noting that
ε =
ε0 +
εpe for
σys >
σys0, this reads
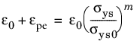 for
for 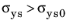
which is equivalent to Swift isotropic hardening, when the strain hardening exponent reads
n =
1/m