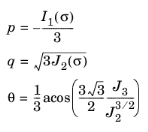The Cam-clay material model was developed in the 1970s at the University of Cambridge, and since then it has experienced many modifications. The modified Cam-clay (MCC) model is the most commonly used model due to its smooth yield surface, and it is the one implemented in COMSOL Multiphysics.
The modified Cam-clay model is a so-called critical state model, where the loading and unloading of the material follow different paths in stress space. The model also features hardening and softening. Different formulations can be found in textbooks, see for instance
Ref. 68,
Ref. 69, and
Ref. 70.
Here, σm is the
mean stress,
σmises is the von Mises
equivalent stress,
θ is the
Lode angle, and
Γ(
θ) is a function of
θ that defines the shape of the yield function in the
Octahedral Plane.
The shape of the yield function in the Octahedral Plane,
Γ(
θ), can be made a function of the Lode angle
θ by using any of the functions described in
Octahedral Section. The most common choice,
Γ(
θ) = 1, results in a circular section that recovers the original Cam-clay model.
The parameter pc > 0 is the
consolidation pressure, and the parameter
M > 0 defines the slope of the
critical state line in the
Meridional Plane which also represents the eccentricity of the ellipse. This parameter can be matched to the friction angle
ϕ in the
Mohr–Coulomb Criterion criterion as
(3-130)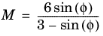
The parameter MQ represents the slope of the
critical state line for the plastic potential, which a can be matched to the
Mohr–Coulomb Criterion criterion at the compressive meridian by the dilatation angle
ψ
|
|
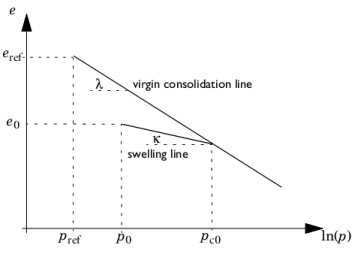
The void ratio e is the ratio between the pore space and solid volume. It can be written in terms of the porosity ϕ as e = ϕ/(1 − ϕ).
|
The compression index λ corresponds to the slope of the
virgin isotropic consolidation line, and the swelling index
κ corresponds to the slope of the
swelling line (also called unloading-reloading line) in the
e versus
ln(
p) plane. The reference void ratio
eref is measured at the reference pressure
pref and the initial void ratio
e0 is measured at the initial mean stress
p0. The starting value of the initial mean stress
p0 is the reference pressure
pref. The equation for the virgin isotropic consolidation line reads
where e0 is the initial void ratio calculated as
|
|
The initial void ratio e0 can be directly entered as user input. In this case, the void ratio at the initial consolidation pressure, ec0, is not needed as intermediate variable.
|
(3-131)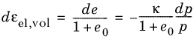
Integrating Equation 3-131, the equation is reformulated as
(3-132)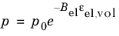
|
|
The contribution to initial mean stress p0 also comes from the mean stress in the initial or external stress tensor. The reference pressure is generally a unit pressure in the used unit system, in the literature the value varies from 1 kPa to 100 kPa. In COMSOL Multiphysics the default value is 100 kPa.
|
At zero volumetric elastic strain and with zero contribution from the Initial Stress and Strain or
External Stress features, the initial mean stress is nonzero and equal to the reference pressure
pref. The reference pressure acts as an
in situ stress.
(3-133)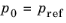
The secant bulk modulus Ks (or bulk modulus
K) is written as
(3-134)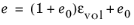 or
or
(3-135)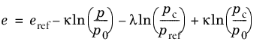
Equation 3-134 is used to compute the void ratio, which matches the analytical expression in
Equation 3-135. These two equations can be used for verification purposes.
In the modified Cam-clay model, hardening is controlled by the consolidation pressure pc, which depends on the volumetric plastic strain
εp,vol as
(3-136)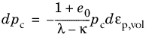
The evolution of the consolidation pressure depends on the values for the initial void ratio e0, the
swelling index κ, and the
compression index λ, which are positive parameters that fulfill
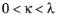 and
and 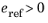
|
|
If an Initial Stress and Strain or External Stress node is added, the initial consolidation pressure pc0 must be larger than the mean initial (or external) stress, otherwise the initial stress state will be outside the Cam-clay yield surface.
|
Here, σ is the stress tensor,
ε is the total strain tensor,
εel is the elastic strain tensor, and
G is the shear modulus.
At zero volumetric strain, and with zero contribution from Initial Stress and Strain or
External Stress features, the pressure in the MCC model is equal to the reference pressure
pref (see
Equation 3-132 and
Equation 3-133). This is needed since the MCC model does not have stiffness at zero stress. The reference pressure appears as an additional term in the variational formulation (weak equation).
The plastic strain tensor εp is computed from the flow rule
where λp is the plastic multiplier and the derivatives of the plastic potential
Qp with respect to the stress tensor
σ. An associated flow rule is used such that
Qp =
Fy.
This relation explains why there is isotropic hardening when the pressure is
p > pc/2 and
isotropic softening when
p < pc/2. As opposed to what happens in
Metal Plasticity, in the modified Cam-clay soil model the volumetric plastic strain can either increase or decrease as plastic deformation occurs.
When an external pore pressure pf is added to the MCC material, the yield function is shifted along the
p axis.
The quantity p − pf is normally regarded as the
effective pressure, or effective stress, which should not be confused with the equivalent von Mises stress. To add the effect of a fluid pressure in the pores to the modified Cam-clay material, add an
External Stress feature.
The structured Cam-clay (SCC) model (
Ref. 76) was developed to circumvent the limitations of the Cam-clay model when applied to structured soils and clays. The SCC model, however, does not consider the influence of the soil structure neither on strength characteristics (especially cohesion) nor in the softening behavior, and it is also not suitable to model cemented clays.
The modified structured Cam-clay (MSCC) model was further developed to model destructured, naturally structured and artificially structured clays (
Ref. 75), and it is the one implemented in COMSOL Multiphysics.
In the MSCC model, the reduction of mean effective stress due to structure degradation, pb, depends on the equivalent plastic strain
εpe. The destructuring mechanism is the process of reducing structure strength due to the degradation and crushing of the structure. The structure degradation is given by
(3-137)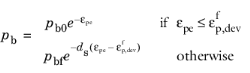
Here, pb0 is the initial structural strength,
pbf the failure structural strength,
εfp,dev is the plastic deviatoric strain at failure, and
ds is the
destructuring index due to shear deformation.
where is e is the void ratio of the structured clay,
Δe is the
additional void ratio, and
e* is the
void ratio of the destructured clay at the same stress state. The void ratio is computed by using
Equation 3-135. Further,
Δec0 is the
additional void ratio at preconsolidation pressure, and
dv is the
destructuring index due to volumetric deformation.
Here, θ is the
Lode angle, and
Γ(
θ) is a function of
θ that defines the shape of the yield function in the
Octahedral Plane.
The shape of the yield function in the Octahedral Plane,
Γ(
θ), can be made a function of the Lode angle
θ by using any of the functions described in
Octahedral Section. The most common choice,
Γ(
θ) = 1, results in a circular section that recovers the original criterion.
The parameter MQ represents the slope of the
critical state line for the plastic potential, which a can be matched to the
Mohr–Coulomb Criterion criterion at the compressive meridian by the dilatation angle
ψ
Here, ς is a parameter to smooth the shape of the plastic potential. The slope of the critical state line,
MQ, is found by using
Equation 3-130.
Here, λ* is the
compression index for destructured clay,
κ is the
swelling index, and
η is ratio of shear stress to mean stress.
(3-138)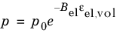 with
with 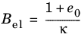
At zero volumetric strain, and with zero contribution from the Initial Stress and Strain or
External Stress features, the pressure in the MSCC model is equal to the reference pressure
pref (see
Equation 3-138 and
Equation 3-133). This is needed since the MSCC model does not have stiffness at zero stress. The reference pressure appears as an additional term in the variational formulation (weak equation).
The Barcelona basic model (BBM) was developed to simulate the loading of unsaturated and partially saturated soils, by incorporating an extra state variable for the pore suction. The suction value depends on the amount of water in the soil, and it affects the flow in porous soils as well as the deformation and stress distribution.
The BBM model uses the concepts of plasticity theory, incorporating the critical state model (Ref. 77). This soil model matches the results obtained with the modified Cam-clay model in fully saturated soils.
The so-called extended Barcelona basic model (BBMx) was further developed to overcome numerical limitations in the original BBM model (
Ref. 78). The model implemented in COMSOL Multiphysics follows
Ref. 78 with certain modifications described in this section.
Here, p and
q are stress invariants as defined in
The Modified Cam-Clay Soil Model,
pcs is the consolidation pressure at current suction,
ps is the tensile strength due to current suction,
s is the current suction,
b is a dimensionless smoothing parameter,
sy is the yield value at current suction, and
pref is the reference pressure at which the reference void ratio
eref was measured.
The shape of the yield function in the Octahedral Plane,
Γ(
θ), can be made a function of the Lode angle
θ by using any of the functions described in
Octahedral Section. The most common choice,
Γ(
θ) = 1, results in a circular section that recovers the original criterion.
The tensile strength due to current suction, ps, is linearly related to the suction level as
ps =
ks, where
k is the tension to suction ratio.
The parameter MQ represents the slope of the
critical state line for the plastic potential, which a can be matched to the
Mohr–Coulomb Criterion criterion at the compressive meridian by using the dilatation angle
ψ
Here, ς is a parameter to smooth the shape of the plastic potential. The slope of the critical state line,
MQ, is found by using
Equation 3-130.
where λ(s) is the compression index at current suction,
λ0 is the compression index at saturation, and
κ is the swelling index. The compression index at current suction,
λ(s), is given by
where w and
m are weighting and soil stiffness parameters.
The slope of the critical state line M can be computed from the Matsuoka–Nakai criterion, in which case it depends on both the Lode angle
θ and the angle of internal friction
ϕ
(3-139)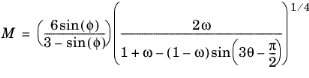
At the tensile or compressive meridians, where the Lode angle is θ =
0 or
θ =
π/3, the slope of the critical state line achieves the same expression as when matched to the
Mohr–Coulomb Criterion, see
Equation 3-130
As in The Modified Cam-Clay Soil Model, hardening is controlled by the evolution of the consolidation pressure
pc, which depends on the volumetric plastic strain
εp,vol.
(3-140)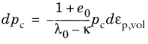
The initial void ratio e0, the swelling index
κ, and the compression index at saturation
λ0, are positive parameters.
The evolution of the yield value at current suction, sy, is also governed by the volumetric plastic strain
εpl,vol as
(3-141)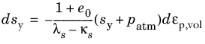
Here, λs is the compression index for changes in suction,
κs is the swelling index for changes in suction, and
patm is the atmospheric pressure, all positive parameters. Note that
Equation 3-140 and
Equation 3-141 are normally given with opposite sign. Here, however, the structural mechanics convention is used, so the increments in consolidation pressure and suction are positive in compression.
Here K is the bulk modulus, and
Kcs the stiffness to suction. Note that the pressure
p in compression and suction
s is positive variables, but the elastic volumetric strain
εel,vol is negative in compression. The volumetric elastic response due to suction is given by
Here, s0 is the initial suction. The volumetric elastic response due to suction is accounted as an inelastic strains in the total strain tensor, any changes in suction while keeping a constant pressure can cause volumetric strains.
(3-142) with
with 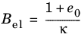
At zero volumetric strain, and with zero contribution from the Initial Stress and Strain or
External Stress feature, the pressure in the BBMx model is equal to the reference pressure (see
Equation 3-142 and
Equation 3-133). This is needed since the BBMx model does not have stiffness at zero stress. The reference pressure appears as an additional term in the variational formulation (weak equation form).
|
|
The material property λ0 is the compression index at saturation, which does not depend on suction.
The variable λ(s), which is a function of the current suction, corresponds to the compression index (slope) in the void ratio versus mean stress plot (log axis).
The material property λs corresponds to the compression index (slope) in the void ratio versus matrix suction plot (log axis), which does not depend on the mean stress.
|
The hardening soil model is an elastoplastic material model with a stress and stress path-dependent stiffness. It is a so-called
double stiffness model, meaning that the soil stiffness is different during primary loading and unloading/reloading load paths (
Ref. 79).
In Ref. 81, the shear hardening and failure surfaces are combined, and the failure surface imposes the final limit on shear stresses. COMSOL Multiphysics implements the latter version.
The 50% failure stiffness for primary loading,
E50, and the
stiffness for unloading and reloading,
Eur, are used to define the elastic relation and hardening variable. These are given by
Here 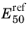 is the reference failure stiffness
is the reference failure stiffness for primary loading at reference pressure,
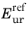
is the
reference stiffness for unloading and reloading at reference pressure,
c is the cohesion,
ϕ is the friction angle, and
m is the stress exponent.
The ultimate deviatoric stress qf and the stress to failure
qa are derived from the
Mohr–Coulomb Criterion
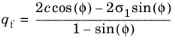 and
and 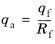
where Rf is the failure ratio.
Here, θ is the
Lode angle, and
Γ(
θ) is a function of
θ that defines the shape of the yield function in the
Octahedral Plane, and
ψm is the
mobilized dilatancy angle.
The shape of the yield function in the Octahedral Plane,
Γ(
θ), can be made a function of the Lode angle
θ by using any of the functions described in
Octahedral Section. The most common choice,
Γ(
θ) = 1, results in a circular section.
where Kc is the hardening modulus and
The dilatancy cutoff is implemented by setting the mobilized dilatancy angle ψm equal to zero when the void ratio reaches the critical void ratio
emax.
where C is a function of the stiffness modulus
Eur and Poisson’s ratio
ν.
The mobilized dilatancy angle ψm is explicitly used in the definition for the plastic potential
Qp. Different authors define this variable using different expressions. The original expression for the mobilized dilatancy derived by Rowe (
Ref. 79) is
(3-143)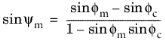
here, ϕc is the
critical friction angle and
ϕm is the
mobilized friction angle, and these are derived from
where ψ is the dilatancy angle,
σi are the principal stresses,
c is the cohesion, and
ϕ is the angle of internal friction.
(3-144)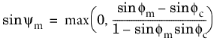
Other expressions (Ref. 79) for the mobilized dilatancy angle include the Wehnert correction
(3-145)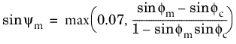
(3-146)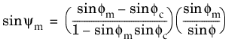
The hardening soil small strain model is a combination of
Small-Strain Overlay model and
The Hardening Soil Model.
The critical shear strain, defined as
Here, Gur is the shear modulus for unloading/reloading, as defined in
The Hardening Soil Model.