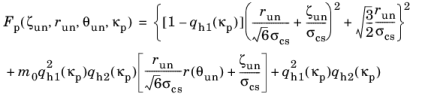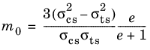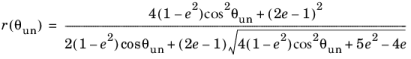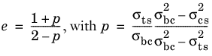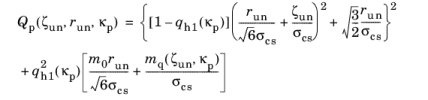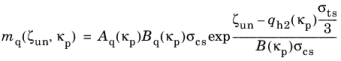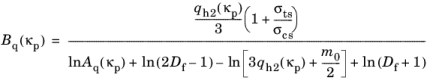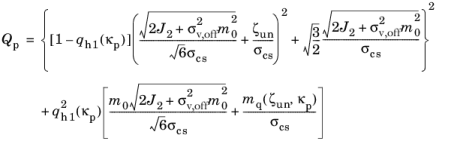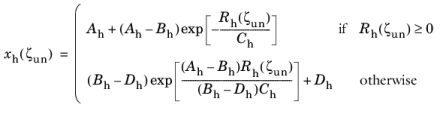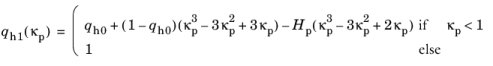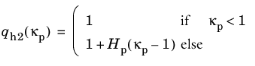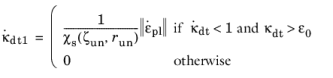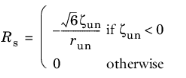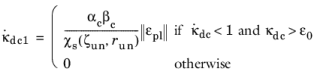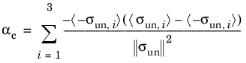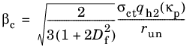The general constitutive equations for the coupled damage–plasticity model uses the concept of the damaged stress tensor
σd and the
undamaged stress tensor
σun. The former is used in the weak formulation while the latter describe the behavior of the intact material.
where σun is split into a positive and negative part by a spectral decomposition in order to account for the anisotropic behavior of concrete in tension and compression. For the same reason, two damage variables introduced: the tensile damage variable
dt and the compressive damage variable
dc. These variables introduce a weakening of the material’s stiffness, and varies from 0 for an undamaged state to 1 for a fully damaged state. Their definitions are described in
Damage Model.
where, C is the fourth order
elasticity tensor, “:” stands for the double-dot tensor product (or double contraction). The elastic strain
εel is the difference between the total strain
ε and inelastic strains
εinel. The coupled damage–plasticity model always adds a plastic strain tensor
εpl to
εinel, but other contributions such as thermal strains can also be considered. There may also be an external stress contribution
σex, with contributions from initial, viscoelastic, or other inelastic stresses. See also
Inelastic Strain Contributions.
The yield function uses a generalization of Willam–Warnke Criterion written as a function of the hardening variable and
κp, and the undamaged stress given in the
Haigh–Westergaard Coordinates (
ξun, r
un,
θun)
(3-114)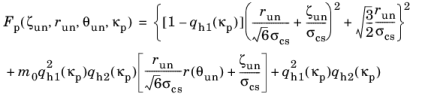
here, qh1(
κp) and
qh2(
κp) are hardening functions, and
σcs is the
uniaxial compressive strength. The friction parameter
m0 is written as
where σts is the
uniaxial tensile strength and
e is the
eccentricity parameter.
The meridians of the yield surface Fp on the
Meridional Plane are parabolic, while the section on the
Octahedral Plane is triangular at low confinement and changes toward a circular shape at high confinement. The shape of the section is given by a dimensionless function of the undamaged Lode angle
θun
As suggested in Ref. 79 and
Ref. 80, the eccentricity is computed as
where σbc is the
biaxial compressive strength.
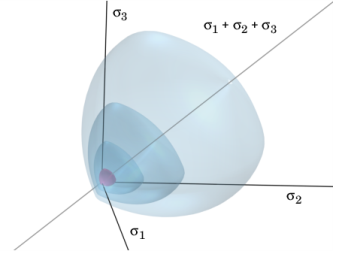
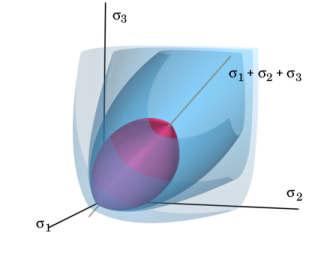
A graphical representation of yield surface Fp = 0 in the undamaged principal stress space and its evolution after hardening is shown in
Figure 3-25 and
Figure 3-26.
(3-115)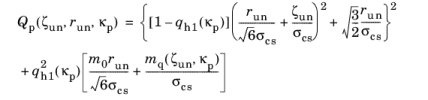
where Aq(
κp) and
Bq(
κp) are auxiliary functions derived from the plastic flow in the post-peak regime, see
Ref. 80. The functions are defined as
where Df is a model parameter that controls the dilatancy of the plastic flow. By default its value reads
Df = 0.85.
The plastic potential in Equation 3-115 leads to a singularity at the point where the plastic potential intersects the hydrostatic axis. Such formulations are not suitable for a numerical implementation. To overcome this, COMSOL Multiphysics modifies
Equation 3-115 such that
where J2 is the second invariant of the undamaged stress tensor. The smoothing parameter
σv,off controls the distance between where the potential in
Equation 3-115 and the smooth potential intersects the hydrostatic axis as exemplified in
Figure 3-18 for Drucker–Prager criterion. The parameter
σv,off can be estimated as a fraction of the uniaxial compressive strength
σcs.
The rate of κp depends on the direction of loading such that it grows faster in uniaxial compression, while it is constant in uniaxial tension. The rate of
κp is, furthermore, scaled by a
ductility measure
The hardening variable κp enters the two hardening functions
qh1 and
qh2 that appear in
Equation 3-114 and
Equation 3-115. These functions control the evolution of the size and shape of the yield function and the plastic potential. They are defined as
where qh0 defines the initial yield limit, and
Hp is a dimensionless hardening modulus that controls the hardening in the post-peak regime. Both parameters should be positive and fulfill the inequality
Hp + qh0 < 1.
The definition of the two damage variables, dt and
dc, are defined in the framework of isotropic damage mechanics, It can described by a damage loading function
Fdi and Kuhn–Tucker loading-unloading conditions
(3-116)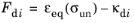
(3-117)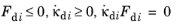
where the index i =
t,
c stands for tension or compression, respectively. In
Equation 3-116,
εeq stands for the equivalent strain and
κdi is a history variable.
where κdi1 and
κdi2 are additional history variables.
where ε0 =
σts /
E. Noteworthy is that the equivalent strain
εeq reduces to
or directly as εeqt =
εeq. The definition of
κdt then follows from
Equation 3-116 and
Equation 3-117.
Two additional history variables, κdt1 and
κdt2, are introduced to account for how damage evolves during different stress states. The variable
κdt1 is a function of the rate of the plastic strain tensor and it is given by the evolution equation
The variable κdt2 is a function of
κdt given by
(3-118)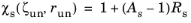
In uniaxial compression, the variables read Rs = 1 and
χs =
As, which can be useful for calibrating the parameter
As. COMSOL Multiphysics by default uses
As = 10.
The definition of the history variable κdc then follows after
Equation 3-116 and
Equation 3-117. The two additional history variables
κdc1 and
κdc2 are introduced to account for damage evolution at different stress states. The variable
κdc1 is a function of the rate of the plastic strain tensor,
and the variable κdc2 is a function of
κdt given by
The factor αc is introduced to distinguish between tensile and compressive stresses, and follows from the spectral decomposition of the undamaged stress
σun as
where σun,i is the
ith principal value of
σun, and the operator
< ·
> denotes the Macaulay brackets. Note that
αc varies from 0 in pure tension to 1 in pure compression.
The factor βc is introduced to accomplish a smooth transition between the case of pure damage to damage–plasticity softening, which may occur during cyclic loading. It is defined as
where Df is the same model parameter used for the plasticity flow. The ductility measure
χs is defined in
Equation 3-118.
Given the history variables, the definition of the damage variables dt and
dc follows the same derivation. Assuming monotonic and uniaxial loading, the damaged stress in the softening regime is described by an enhanced inelastic strain,
εinel,d,
(3-119)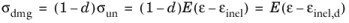
(3-120)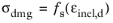
where fs(·) is the
softening law often referred to as the
traction–separation law, here given in a terms of inelastic strains.
Since damage is an irreversible process, it is postulated that the inelastic strain εinel,d can be described by the damage history variables. This strain measure is called the
inelastic damage strain (or crack-opening strain) and it is defined as
Replacing ε –
εinel in
Equation 3-119 with
κd such that
and using it together with Equation 3-120 results in an equation for the damage variable in terms of the history variables of the form
(3-121)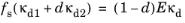
This nonlinear equation is solved for d using Newton’s method at each material point. COMSOL Multiphysics provides a number of built-in softening functions
fs(·) for both tension and compression:
These are depicted in a Figure 3-27. The linear and bilinear definitions have a closed-form solution to
Equation 3-121, which makes them computationally attractive.

When combined with the crack-band method, the stress versus strain curves in Figure 3-27 are defined in terms of stress versus displacement. The stress versus displacement curves are then converted to unique stress versus strains curves at each material point using the crack-band width
hcb, see
The Crack Band Method.
In addition to the built-in softening laws, COMSOL Multiphysics allows user-defined definitions of fs(·). Use the variables
<phys>.<feat>.<feat>.edmgt and
<phys>.<feat>.<feat>.edmgc to defined the damaged strain in tension and compression, respectively. The user-defined function should resemble that in
Figure 3-27 with stress and strain interpreted as positive variables in tension and compression.
assuming that the crack-band method is used. COMSOL Multiphysics provides the variables <phys>.<feat>.<feat>.wdmgt and
<phys>.<feat>.<feat>.wdmgc for the damaged displacement in tension and compression, respectively. For both options, the nonlinear equation is solved to find
d.