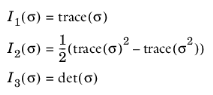Invariants of the Stress Tensor
The different invariants of the stress tensor form an important basis for constitutive models and also for interpretation of stress results. The three fundamental invariants for any tensor are
(3-9)
In many cases, the invariants of the deviatoric stress tensor are also useful.
(3-10)
As defined above J2 ≥ 0. In many material models, the most relevant invariants are I1, J2, and J3. I1 represents the effect of mean stress, J2 represents the magnitude of shear stress, and J3 contains information about the direction of the shear stress.
In tensor component notation, the invariants can be written as
The pressure is defined as
and is thus positive in compression.
•
The internal variables for the invariants I1, I2, and I3 are named solid.I1s, solid.I2s, and solid.I3s, respectively.
•
The internal variables for the invariants J2 and J3 are named solid.II2s and solid.II3s, respectively.
•
The internal variable for the pressure is solid.pm.
Principal Stresses
The principal stresses are the eigenvalues of the stress tensor, computed from the eigenvalue equation.
The three principal stresses are ordered so that
This ordering is true also for the 2D cases. The corresponding principal directions vpi are orthonormal.
•
The internal variables for the principal stresses are named solid.sp1, solid.sp2, and solid.sp3.
•
The internal variables for the components of the directions of the first principal stress are named solid.sp1x, solid.sp1y, and solid.sp1z. The direction vectors for the other two principal stresses are named analogously.
In terms of the principal stresses, the stress invariants can be written as
The principal stresses are the roots of the characteristic equation (Cayley–Hamilton theorem)
The expressions described in Equation 3-9 and Equation 3-10 enter into expressions that define various kind of yield and failure surfaces. A yield surface is a surface in the 3D space of principal stresses that circumscribe an elastic state of stress.
Haigh–Westergaard Coordinates
It is possible to define other variables in terms of the principal invariants. One common auxiliary variable is the Lode angle θ.
(3-11)
The Lode angle is part of a cylindrical coordinate system called the Haigh–Westergaard coordinates. The height (in the hydrostatic axis direction) corresponds to and the radius corresponds to .
The Lode angle is bounded to 0 ≤ θ ≤ π/3 when the principal stresses are sorted as σp1 ≥ σp2 ≥ σp3 (Ref. 51). Following this convention, θ = 0 corresponds to the tensile meridian, and θ = π/3 corresponds to the compressive meridian.
The principal stresses (σp1, σp2, and σp3) are then written in terms of the invariants I1, J2, and the Lode angle θ as:
 
The Lode angle is undefined at the hydrostatic axis, where all three principal stresses are equal (σp1 = σp2 = σp3 = I1/3) and J2 = 0. To avoid division by zero, the Lode angle is actually computed from the inverse tangent function atan2, instead of the inverse cosine, as stated in Equation 3-11.
The Lode angle and the equivalent (von Mises) stress can be called in user defined yield criteria by referencing the variables solid.thetaL and solid.mises, where solid is the name of the physics interface node.
Octahedral Plane
The octahedral plane (also called π-plane or deviatoric plane) lies perpendicular to the hydrostatic axis in the Haigh–Westergaard Coordinates. The stress normal to this plane is σoct =  I1/3, also called mean stress or hydrostatic stress, and the shear stress on that plane is defined by .
The profile of the yield surface on the octahedral plane is useful for visualizing changes in yield limits under compression or tension, and it illustrates how the criterion depends on the Lode angle. See for instance the Tresca Criterion and the Mohr–Coulomb Criterion.
Meridional Plane
The meridional plane, also called Rendulic plane, is the profile of the yield criterion at a given Lode angle, typically at the compressive meridian θ = π/3.
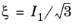
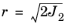
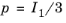
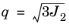
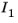
In the Haigh–Westergaard Coordinates, the meridional plane is given by the coordinates and , but it also common to visualize criteria in the pq-plane, given by the coordinates and , or the plane given by the axes and .
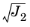