Many materials exhibit a distinct elastic regime where deformations are recoverable and path-independent. This elastic behavior can be modeled using a Linear Elastic Material,
Nonlinear Elastic Materials, or
Hyperelastic Materials models. In elastoplasticity, the elastic regime is constrained by the
yield limit in stress space. When stresses exceed this limit, permanent inelastic strains develop, which, unlike elastic strains, remain even after the stresses are removed.
For elastoplastic materials, the emphasis is primarily on models that capture inelastic strains developing independently of loading rate, known as rate-independent plasticity models. This class of models effectively describes many engineering materials, including homogeneous or porous metals at low temperatures, as well as soils.
In contrast, rate-dependent elastoplastic material models, such as creep and viscoplasticity material models, are commonly applied in scenarios involving high temperatures, where a clear yield limit is difficult to define, or under conditions of high loading rates. For more details on these models, refer to
Creep and Viscoplasticity.
(3-49)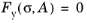
where σ is the total stress tensor and
A is a set of hardening forces. In case of a geometrically nonlinear case,
σ is typically identified as the Cauchy stress tensor. The hardening forces depend on the hardening variables
α. In many cases there is only a single hardening force, the scalar yield stress
σys. The yield function then reads
(3-50)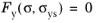
The elastic domain is defined as the set of stresses for which the yield function
Fy is smaller than zero, that is
For stresses in Ωe no plastic deformation occurs. However, for stresses on the boundary of the elastic domain, where
Fy = 0, plastic deformation may occur. This boundary is called the
yield surface, which is represented by a hypersurface in stress space. It can be defined as
The flow rule defines the evolution of the plastic deformation. The flow rule is defined in terms of a
plastic potential Qp, which is given on the same general form as the yield function
The gradient of the plastic potential Qp with respect to the stress tensor
σ gives the direction of plastic flow as
For associated plastic flow, the plastic potential equals the yield function, that is
(3-51)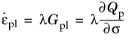
Here, λ is the
plastic multiplier, which is a non-negative variable that satisfies the complementarity condition
λFy = 0. The latter condition states that plastic flow may only occur when the stress is
on the yield surface.
|
|
When additive plasticity is used and the Include geometric nonlinearity checkbox is selected in the study Settings window, the Cauchy stress tensor is used to evaluate the yield function and plastic potential. Plastic flow is, however, assumed to be in the direction of the second Piola–Kirchhoff stress tensor, and the computed plastic strain tensor can be interpreted as a Green–Lagrange strain.
|
When a multiplicative decomposition of deformation is used, COMSOL Multiphysics characterizes plastic deformation through the plastic right Cauchy–Green tensor Cp, or more precisely its inverse
Cp-1. However, the internal variable is the inverse of the (symmetric) plastic stretch tensor,
Up-1, such that
Cp-1 =
Up-2. An exception is when kinematic hardening is included. Then plastic deformation is characterized by the inverse of the (nonsymmetric) plastic deformation tensor,
Fp-1. See
Kinematic Hardening for details.
In a multiplicative formulation of plasticity (Ref. 90,
Ref. 91, and
Ref. 92), the plastic flow rule can be written as the
Lie derivative of the elastic left Cauchy–Green deformation tensor
Bel:
(3-52)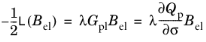
As for the Additive Plastic Flow,
λ represents the plastic multiplier, which is a non-negative variable that satisfies the complementarity condition
λFy = 0. The latter condition states that plastic flow may only occur when the stress is on the yield surface.
The Lie derivative of Bel is then expressed in terms of the rate of the plastic right Cauchy–Green tensor
(3-53)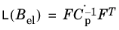
By using Equation 3-52 and
Equation 3-53, the plastic flow rule is written as (
Ref. 91)
(3-54)
The evolution of the hardening variables is described by the hardening rule. Similarly to the flow rule, the hardening rule for a set of hardening variables
α is postulated as
(3-55)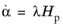
Here, Hp(
σ,
A) is a general hardening modulus that describes how the hardening variables evolve with plastic deformation.
(3-56)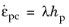
The equivalent plastic strain εpe is then used to define how the yield stress
σys evolves during plastic flow, that is,
σys is the thermodynamic force conjugate to
εpe. See
Isotropic Hardening for more details.
The hardening modulus hp may take different forms, and it can be specified in a user defined expression.
A common assumption follows from the concept of strain hardening, where the definition of a von Mises equivalent strain is used
Another approach is to derive the hardening modulus hp from a potential, analogous to how plastic flow is defined by taking the gradient with respect to its conjugate hardening force. Here, we assume an associated hardening law, such that
(3-57)
Here, the superscript n+1 indicates a variable evaluated at the current parameter or time step, and a superscript
n denotes a variable with values form the previously converged step.
Also, U represents other dependent variables in the model, such as displacements, that are held fixed within the plastic algorithm, the vector
q
|
c
|
If Fy ≤ 0, the stress is elastic and no more steps are necessary. Otherwise the predictor solution is not admissible, and the algorithm continues to the corrector step.
|
In most plasticity features it is also possible to force the use of line search iterations by setting the Local method to
Backward Euler, damped. This setting is available in the
Advanced section. When selected, it is possible to specify the
Maximum number of line search iterations. A common value is 4. It is important to note that an excessive number of line search iterations can cause the algorithm to stall.
When using the multiplicative decomposition, the inverse of the plastic stretch tensor Up-1 is the internal variable used to characterize plastic deformation. In general COMSOL Multiphysics here also applies the so-called exponential mapping technique to discretize the plastic flow rule in
Equation 3-54 as
The singe yield function in Equation 3-49 is then extended to a set of
n yield functions such as
COMSOL Multiphysics implements multisurface plasticity models by converting the set of yield functions into a single smooth and C2 differentiable function. This is done by using the procedure outlined in
Ref. 115. The same procedure is applied for combining a set of
n plastic potentials.
To address this, an iterative approach is employed, where n yield functions are combined into a single smooth function
Fysn-1.
Here, s(x) is a smooth function defined as
where a is a smoothing parameter, and
g(x) is a function that fulfills certain requirements among them being
C2 differentiable. A simple function that meets these requirements is the trigonometric function (
Ref. 115)
The smoothing parameter a is then related to the offset of the smooth function
Fysn-1 from the nonsmooth function
Fy at the intersections of two or more functions
Fysk.
|
|
When the Calculate dissipated energy checkbox is selected, the plastic dissipation density is available under the variable solid.Wp and the total plastic dissipation under the variable solid.Wp_tot.
|
The nonlocal plasticity model implemented in COMSOL Multiphysics is based on the implicit gradient method suggested in
Ref. 113, and it incorporates some of the generalizations introduced by the micromorphic theory (
Ref. 114).
The theory assumes that the free energy of the elastoplastic material depends on both the macroscopic displacement u and other macrostate variables, such as the equivalent plastic strain
εpe, and also on some microstate variable.
(3-58)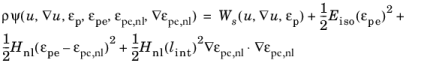
where Ws is the elastic free energy,
Hnl is a model parameter that determines the strength of the coupling between the macro and micro states, and
lint is the length scale that determines the influence radius of the interaction.
For simplicity, Equation 3-91 assumes linear isotropic hardening, but the same concept is applicable for more general hardening laws, and it can also be extended to kinematic hardening.
Taking the variation of Equation 3-91 with respect to the state variables
εpe,
εpe,nl, and
∇εpe,nl leads to the following set of equations related to the plasticity model:
here, Ω represents the domain of the elastoplastic problem.
The variation of Equation 3-91 with respect to the remaining state variables leads to the standard elasticity equations. In the nonlocal (or regularized) plasticity problem,
εpe,nl is an additional dependent variable that is solved as part of the global problem.
Add a Set Variables subnode to
Metal Plasticity,
Porous Plasticity,
Pressure-Dependent and Soil Plasticity, or
Elastoplastic Soil Models to set up the plastic strain tensor, plastic deformation gradient, the equivalent plastic strain, and other internal variables.
The von Mises criterion suggests that yielding of the material occurs when the second deviatoric stress invariant
J2 reaches a critical value
k. Hence, von Mises plasticity is often also referred to as
J2 plasticity. It can be written in terms of the elements of Cauchy’s stress tensor (
Ref. 51)
where σys is the uniaxial
yield stress level and
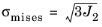
is the equivalent von Mises stress. An associative flow rule is always used for the von Mises criterion, that is,
Qp =
Fy
The Tresca criterion suggests that yielding occurs when the maximum shear stress reaches a critical value. Given a spectral decomposition of Cauchy’s stress tensor, the maximum shear stress is expressed as
where σ1 is the maximum principal stress and
σ3 is the minimum principal stress. The Tresca criterion then reads
where τys is the shear yield stress. Alternatively, it can be expressed using the uniaxial yield stress
σys, as for the von Mises criterion, and then reads
(3-59)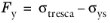
where σtresca =
σ1 − σ3 is the equivalent Tresca stress.
|
|
The Tresca equivalent stress, σtresca = σ1 − σ3, is implemented in the variable solid.tresca, where solid is the name of the physics interface node.
|
Graphically, the Tresca yield surface is represented by an infinite hexagonal prism in principal stress space with it axis coinciding with the hydrostatic axis, see Figure 3-15. The elastic domain corresponds to the inside of the hexagon. The shape of the hexagonal yield surface can be further visualized by projecting it onto the
Octahedral Plane as shown in
Figure 3-16. The upper limit in this surface corresponds to the von Mises yield surface.
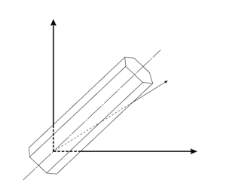
For the case of associated plastic flow, COMSOL Multiphysics constructs a smooth plastic potential to handle the edges of the hexagonal yield function, by using the procedures outlined in Multisurface Plasticity. In general, a full representation of the hexagon requires six yield functions combined into one. However, since the principal stresses are sorted such that
σ1 >
σ2 >
σ3, it is sufficient to consider three functions only
Hill (Ref. 93,
Ref. 94) proposed a quadratic yield function given by the principal axes of orthotropy
ai in a local coordinate system. The yield function can be written in terms of the elements of Cauchy’s stress tensor as
Here, σ is the vector representation of the stress tensor in Voigt order, see
Orthotropic and Anisotropic Materials. The symmetric 6-by-6 matrix reads
where the parameters F,
G,
H,
L,
M, and
N are related to the state of anisotropy.
|
|
Hill plasticity is an extension of J2 (von Mises) plasticity, in the sense that it is volume preserving. Due to this property, six parameters are needed to define orthotropic plasticity, as opposed to orthotropic elasticity, where nine elastic coefficients are needed.
|
with σys =
σys0 if there is no isotropic hardening.
Here, σm is the
mean stress,
σmises is the von Mises
equivalent stress, and
θ is the
Lode angle.
The Pressure-Dependent Plasticity and
Soil Plasticity features implement a number of plasticity models that can be described by a yield function of either a parabolic form
(3-60)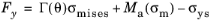
(3-61)
Here, Γ(
θ) is a function of the
Lode angle θ that defines the shape of the yield function in the
Octahedral Plane. The most common choice,
Γ(
θ) = 1, results in a circular section. Similarly,
Ma(
σm) and
Mb(
σm) are functions of the
mean stress σm that define the shape of the yield function in the
Meridional Plane.
The yield stress σys is here interpreted as the stress level when yielding occurs given
Γ(
θ) = 1 and
σm = 0. Various
Isotropic Hardening models can be added by specifying the yield stress
σys as a function of the equivalent plastic strain
εpe.
The Drucker–Prager criterion is as an extension of the von Mises Criterion to include pressure-dependence. It is available in both the
Pressure-Dependent Plasticity and
Soil Plasticity features and it can be used to model a wide variety of materials.
where a1 is a model parameter that controls the pressure dependence. In this expression, the mean stress
σm corresponds to the negative pressure, that is, it is positive in tension.
(3-62)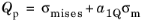
The parameter a1Q controls the influence of pressure on the plastic flow.
The plastic potential in Equation 3-62 leads to a singularity in the flow rule where the yield surface intersects the hydrostatic axis, that is, the tip of the cone. Such formulation is not suitable for a numerical implementation. To handle this, COMSOL Multiphysics modifies
Equation 3-62 such that a smooth plastic potential is obtained with a rounded vertex. The smooth plastic potential is written as
(3-63)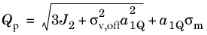
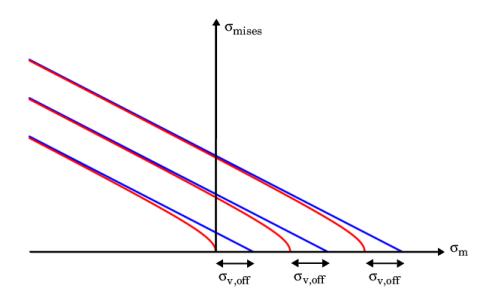
Here, the smoothing parameter σv,off controls the distance where the potential in
Equation 3-62 and the smooth potential in
Equation 3-63 intersect the hydrostatic axis as shown in
Figure 3-18.
For Soil Plasticity, the parameters in Drucker–Prager criterion receive different names to comply with geotechnical conventions. The yield function is written as
The parameters k,
α, and
αQ are generally identified from common soil parameters: cohesion
c; friction angle
ϕ; and dilatation angle
ψ, and by matching the Drucker–Prager criterion to the
Mohr–Coulomb Criterion. This can be done using different assumptions:
The elliptic criterion in Pressure-Dependent Plasticity implements
Equation 3-61 with the meridional shape function parameterized with a linear and a quadratic dependence on the mean stress
σm as
The shape of the yield function in the Octahedral Plane is generally circular, but it can be made a function of the Lode angle
θ by using any of the functions described in
Octahedral Section.
Setting b1 = 0 recovers an ellipse like in for example the Cam–Clay family of models. Parameter
b3 > 0 then represents the shift of the ellipse along the hydrostatic axis, and parameter
b2 gives the aspect ratio of the ellipse in the
Meridional Plane.
Setting b2 = 0 and
b1 > 0 results into a paraboloid that opens into the compressive direction and intersects the hydrostatic axis at
σm =
σys2/
b1. Setting
b1 = 0 and
b2 = 0 recovers the
von Mises Criterion.
with a set of three parameters to control the shape of the plastic potential in the Meridional Plane. For nonassociated flow, the plastic potential is always assumed to be independent of the Lode angle
θ, and its projection on the
Octahedral Plane is thus circular.
The parabolic criterion in Pressure-Dependent Plasticity implements
Equation 3-60 with the meridional shape function parameterized with a linear, a quadratic, and an exponential dependency on the mean stress
σm as
The shape of the yield function in the Octahedral Plane is generally circular, but it can be made as a function of the Lode angle
θ by using any of the functions described in
Octahedral Section.
Setting a1 > 0,
a2 =
a3 = 0 recovers the Drucker–Prager criterion. By setting
a2 > 0,
a1 =
a3 = 0, a closed parabola is obtained similar to, for example, the GAZT criterion for foams.
(3-64)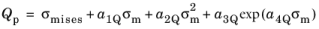
with a set of four parameters to control the shape of the plastic potential in the Meridional Plane. For nonassociated flow, the plastic potential is always assumed to be independent of the Lode angle
θ, and its projection onto the
Octahedral Plane is thus circular.
The plastic potential in Equation 3-64 leads to a singularity in the flow rule where the yield surface intersects the hydrostatic axis, that is, the vertex of the cone. This formulation is not suitable for a numerical implementation. To handle this, COMSOL Multiphysics modifies
Equation 3-64 such that a smooth plastic potential with a rounded vertex is used. The smooth plastic potential is written as
(3-65)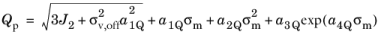
Here, the smoothing parameter σv,off controls the distance between where the potential in
Equation 3-64 and the potential in
Equation 3-65 intersect the hydrostatic axis. If
α1Q = 0, a small fall-back value is used in the square root term of
Equation 3-65. The smooth plastic potential is used for the
associated plastic flow also.
The profile of the yield function on the Octahedral Plane is useful for denoting changes in the yield limit under different loading conditions, for example, compression or tension. COMSOL Multiphysics provides three alternative definitions of the function
Γ(
θ) that controls the shape of the yield function on the octahedral plane:
Gudehus (Ref. 96) proposed an octahedral section that changes with the Lode angle
θ. The change in the cross sectional shape depends on one parameter as
(3-66)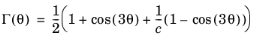
A value of c = 1 represents a circular section. Independent of the value of the parameter
c, the function equals

at the tensile meridian (
θ =
0), and
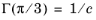
at the compressive meridian. For
c < 1, the tensile strength is lower than the compressive strength. The function
Γ(
θ) is thus an approximation of the ratio of tensile to compressive strength. For the function to be convex, the parameter
c has a lower bound of 7/9 and an upper bound of 9/7.
Panteghini and Lagioia (Ref. 97) proposed a three-parameter function to control the octahedral section based on the Lode angle as follows:
(3-67)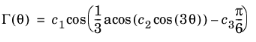
The function was derived with the purpose to recover common soil plasticity yield functions, including a rounded Mohr–Coulomb Criterion, the
Matsuoka–Nakai Criterion, and the
Lade–Duncan Criterion. However, the three parameters of the function provide a flexible option to control the octahedral section in a general manner. Setting the parameter
c2 < 1 creates a continuous and
C2 differentiable function
.
The foam plasticity model in Pressure-dependent plasticity, is an elliptic model that is a generalization of the model first proposed by Deshpande and Fleck (
Ref. 116) to model structural foams. It is popular not only for modeling the failure of metallic foams, but also for battery cells, biological tissue, and other materials with a cellular structure.
(3-68)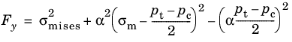
The shape of the ellipse is controlled by three parameters, where pt and
pc define the limits in hydrostatic tension and compression, respectively. The parameter
α controls the aspect ratio of the ellipse, and it is inferred from the initial uniaxial compressive strength
σuc0 such that
Here, pc0 is the initial yield stress in hydrostatic compression when hardening is considered, which means that the aspect ratio of the ellipse is constant after plastic deformation.
(3-69)
Compared to the yield function in Equation 3-68, the centroid of the ellipse defined by the plastic potential in
Equation 3-69 is located at the origin of the
Meridional Plane. The shape of the plastic potential is defined by a single parameter,
β, that controls the aspect ratio of the ellipse. The parameter is defined by the
plastic Poisson’s ratio νp as
Note that εpv is positive in compression.
where pch is a hardening function. A common hardening model for foams is that the compressive yield stress varies with the volumetric strain by a power function, that is, p
ch(εpv) =
C εpvn.
The axial equivalent plastic strain εpa is difficult to identity for general loading conditions. It is therefore estimated from the equivalent volumetric plastic strains
εpv and the plastic Poisson’s ratio
νp as
Note that when volumetric hardening is included, it is only the yield stress in hydrostatic compression pc that evolves with the plastic deformation. All other parameters that define the yield function and plastic potential remain fixed.
The Mohr–Coulomb criterion is a classical and popular criterion in soil mechanics. It was developed by Coulomb before the Tresca and von Mises criteria for Metal Plasticity, and it was the first criterion to include the hydrostatic pressure. The criterion states that failure occurs when the shear stress and the normal stress acting on any element in the material satisfy the equation
were, τ is the shear stress,
c the cohesion, and
ϕ denotes the friction angle.
Here parameters α and
k are defined by the friction angle
ϕ and the cohesion
c as
The choice of these parameters results in the hexagonal pyramid depicted in Figure 3-19 with the sharp corners. If used as plastic potential for the flow rule, this leads to singularities and a formulation not suitable for a numerical implementation. COMSOL Multiphysics defines the smooth plastic potential as
(3-70)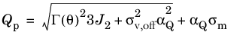
where the vertex is rounded using the same method as for the Drucker–Prager Criterion. The sharp corners of the octahedral section are rounded by setting
c2 =
β with
β < 1 for the plastic potential. This results in a smooth and continuous octahedral section that inscribes the Mohr–Coulomb criterion. The default value is
β = 0.99. Setting a lower value for
β increases the radius of the rounded corners.
The Mohr–Coulomb criterion can be used with either an associated or nonassociated flow rule. For the associated flow rule,
αQ = α such that the pressure dependence of plastic flow is governed by the friction angle
ϕ. When a nonassociated flow rule is used,
αQ is defined by the dilatation angle
ψ as
Matsuoka and Nakai (Ref. 55) discovered that the sliding of soil particles occurs in the plane in which the ratio of shear stress to normal stress has its maximum value, which they called the
mobilized plane. The yield surface is based on the first, second, and third
Invariants of the Stress Tensor as
where the parameter μ =
(τ/
σn)STP equals the maximum ratio between shear stress and normal stress in the
spatially mobilized plane (STP-plane). The invariants are applied over the effective stress tensor, this is, the stress tensor minus the fluid pore pressure.
where ϕ denotes the friction angle.
As shown in Ref. 97, the above formulation of the Matsuoka–Nakai criterion is not suitable for numerical implementation since it results in false elastic domains in the tensile octant’s of the principal stress space.
Here, the parameters α and
k can be defined by the friction angle
ϕ and the cohesion
c as
The Matsuoka–Nakai criterion can be used with either an associated or nonassociated flow rule. For the associated flow rule,
αQ = α, such that the pressure dependence of plastic flow is governed by the friction angle
ϕ. When a nonassociated flow rule is used,
αQ is defined by the dilatation angle
ψ as
where I1 and
I3 are the first and third
Invariants of the Stress Tensor, respectively, and
kLD is a parameter related to the direction of the plastic strain increment in the triaxial plane. It can be derived from the friction angle
ϕ as
As shown in Ref. 97, the above formulation of the Lade–Duncan criterion is not suitable for numerical implementation since it results in false elastic domains in the tensile octants of the principal stress space.
Here, parameters α and
k can be defined by the friction angle
ϕ and the cohesion
c as
The Lade–Duncan criterion can be used with either an associated or nonassociated flow rule. For the associated flow rule,
αQ = α, such that the pressure dependence of plastic flow is governed by the friction angle
ϕ. When a nonassociated flow rule is used,
αQ is defined by the dilatation angle
ψ as
For any parabolic type plasticity models, a cap can be added to the plasticity model to limit the elastic domain in compression. This is of particular interest for models that are linear in the Meridional Plane such as the
Drucker–Prager Criterion, and other soil plasticity models where the yield function opens in the compressive direction of the hydrostatic axis. Normally, these models are not accurate above a given pressure limit, since real-life materials cannot bear infinite loads and still behave elastically. To circumvent this, two types of cap models can be added in COMSOL Multiphysics
The elliptic cap formulation is the most comprehensive, often providing more accurate predictions of observed behavior. However, the simplicity of the
planar cap makes it a practical alternative in some cases. Both formulations employ an associated flow rule and allow for hardening that is independent of the yield functions.
where pc is the
pressure limit. The yield function imposes a pressure limit that restricts any values exceeding
pc.
where pc0 is the
initial pressure limit, and
pch is the
hardening function that depends on the hardening variable
εpc. A
perfectly plastic model assumes
pch = 0.
The yield function of the elliptic cap is a function of stress invariants σm, σmises, and
θ; it only depends on the Lode angle if the parent yield function does. For the most general case, the yield function reads
Where the operator < ·
> represents the Macaulay brackets. The term
Fy(
−pcc,0,0) implies that the parent yield function is evaluated at
σm =
−pcc, and at zero von Mises stress and zero Lode angle,
σmises =
θ = 0.
where pc0 is the initial pressure limit and
pcc0 is the initial location of the centroid on the hydrostatic axis. This definition implies that the aspect ratio is constant also when hardening is included.
Figure 3-22 visualizes the combined yield surface of a Drucker–Prager yield function and the elliptic cap with no hardening on the meridional plane.
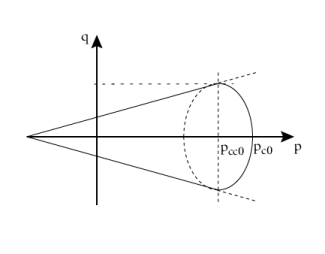
Here pcch is the hardening function that depends on the hardening variable
εpc. However, when the
Drucker–Prager Criterion is used, the hardening model directly specifies the evolution of the pressure limit
pc as
where pc0 is the initial pressure limit and
pch is the hardening function. The current value of the centroid variable,
pcc, is then computed from
pc using geometrical considerations.
The variable εpc is an internal plastic variable added when hardening is included. The additional hardening rule for this variable reads
(3-71)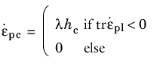
where hc is the hardening modulus.
The condition in Equation 3-71 means that the hardening variable
εpc decreases monotonically with volumetric plastic deformation. However, it is possible to allow the cap to soften. The cap is then limited to move along the compressive part of the hydrostatic axis, and the hardening rule is modified to read
The hardening functions pch and
pcch can be defined by user defined expressions. COMSOL Multiphysics also includes built-in hardening functions intended to model an exponential variation of the material density during compaction.
for the elliptic cap. For both formulations, Kc is the hardening modulus and

is the maximum volumetric plastic strain.
where σm,t is the mean stress limit in tension. The yield function implies that a mean stress exceeding
σm,t is not allowed.
and the applies the procedures outlined in Multisurface Plasticity to construct a smooth and
C2 differentiable yield function
Fcutoff.
An isotropic hardening model typically considers a single scalar hardening variable. COMSOL Multiphysics uses the equivalent plastic strain εpe as described by the hardening rule in
Equation 3-56. By default, most plasticity features assume a strain hardening approach to define
εpe, but other definitions may also be considered.
Isotropic hardening is added to a the general yield function in Equation 3-50 by letting the
yield stress σys be a function of the equivalent plastic strain
εpe. That is, the yield functions reads
where σe is the scalar equivalent stress. COMSOL Multiphysics provides several types of isotropic hardening models for elastoplastic materials:
Here the yield stress is given by the initial yield stress σys0 such that it is constant and independent on the equivalent plastic strain variable
εpe
The yield stress σys(εpe) is for linear isotropic hardening a function of the
equivalent plastic strain εpe and the
initial yield stress σys0
Here, the isotropic hardening modulus Eiso is derived from
For linear isotropic hardening, the isotropic tangent modulus ETiso is defined as (stress increment / total strain increment). The Young’s modulus
E is taken from the parent material model. If the elasticity of the parent material is anisotropic or orthotropic,
E represents an equivalent Young’s modulus.
In the Ludwik model for nonlinear isotropic hardening, the yield stress σys(εpe) is defined by a nonlinear function of the equivalent plastic strain. The Ludwik equation (also called the Ludwik–Hollomon equation) for isotropic hardening is given by the power law
Here, k is the strength coefficient and
n is the hardening exponent. Setting
n = 1 would result in linear isotropic hardening.
Similar to the Ludwik hardening model, the yield stress σys(εpe) is in the Johnson–Cook model defined as a nonlinear function of the equivalent plastic strain
εpe given by a power law. The difference is that effects of the strain rate are included in the model. The yield stress and hardening function is given by
(3-72)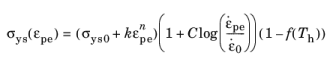
The Johnson–Cook model also adds the possibility to include thermal softening by including a function which depends on the normalized homologous temperature Th. It is a function of the current temperature
T, the melting temperature of the metal
Tm, and a reference temperature
Tref
The strain rate strength coefficient C and the reference strain rate
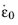
in the Johnson–Cook model are obtained from experimental data. The flow curve properties are normally investigated by conducting uniaxial tension tests in a temperature range around half of the melting temperature
Tm, and subjected to different strain rates like 0.1/s, 1/s, and 10/s.
where the operator < ·
> represents the Macaulay brackets, such that the logarithmic function never evaluates to a negative number. In this formulation, the reference strain rate

must be considered in the quasistatic limit. Below this value, the hardening function will be strain rate independent, but temperature dependent, similar to Ludwik law:
here, k is the strength coefficient,
n is the hardening exponent, and
ε0 is a reference strain. Noting that at zero plastic strain the initial yield stress is related to the strength coefficient and hardening exponent as
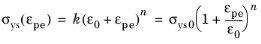 for
for 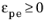
The yield stress σys(εpe) is then defined as
The value of the saturation exponent parameter
β determines the saturation rate of the hysteresis loop for cyclic loading. The
saturation flow stress σsat characterizes the maximum distance by which the yield surface can expand in the stress space. For values
εpe >> 1/β, the yield stress saturates to
where σ∝ is the
steady-state flow stress,
m the saturation coefficient and
n the saturation exponent. For values
mεpen >> 1 the yield stress saturates to
Many engineering materials, particularly metals, exhibit the Bauschinger effect. This phenomenon occurs when a specimen is first loaded in tension until yielding, then unloaded and reloaded in compression. The compressive yield stress is observed to be lower than if the material had been initially loaded in compression. The Bauschinger effect is commonly explained by kinematic hardening, which is one of the primary motivations for incorporating this hardening mechanism in material models.
A kinematic hardening model can be incorporated into the general yield function in Equation 3-50 by shifting the stress tensor
σ by the so-called
back stress σb. The yield function then reads
where σe is the scalar equivalent stress. There are three built-in models to define the evolution of the back stress during plastic deformation:
In the linear kinematic hardening model, also known as Prager’s hardening rule, the evolution the back stress is selected as the hardening variable. The hardening rule is written such that the evolution of the back stress is proportional to the rate of the plastic strain tensor
εpl
(3-73)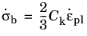
COMSOL Multiphysics assume that the kinematic hardening modulus Ck is constant, in which case no additional equation is solved, and the back stress
σb is defined directly from the plastic strain tensor
where Ek is the kinematic tangent modulus and the Young’s modulus
E is taken from the parent material model. If the elasticity of the parent material is anisotropic or orthotropic,
E represents an equivalent Young’s modulus.
Armstrong and Frederick (Ref. 88) proposed an extension to Prager’s linear kinematic hardening model, by introducing additional terms to
Equation 3-73
(3-74)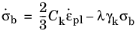
here, γk is a model parameter,
Ck is the kinematic hardening modulus, and
λ is the plastic multiplier. The additional term introduces an effect of saturation in the hardening rule.
Considering this relation, Equation 3-74 is rewritten so that the hardening rule to define the evolution of the back strain reads
Chaboche (Ref. 89) proposed a nonlinear kinematic hardening model based on the superposition of
N back stress tensors
where each of these back stress tensors σb,i follow a nonlinear Armstrong–Frederick kinematic hardening rule
(3-75)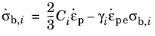
Practitioners would normally select γk = 0 for one of the back stress equations, thus recovering Prager’s linear rule for that branch
The back stress tensor σb is then defined by the superposition of
N back stress tensors
For multiplicative decomposition, the total deformation gradient F is decomposed into an elastic
Fel and a plastic (inelastic) deformation
Fpl
Here Fple is referred to as the “elastic” part of
Fpl, and
Fplv as the “viscous” part of the plastic deformation. Conceptually,
Fple corresponds to a spring and
Fplv to a dashpot that are connect in series in a rheological model. Also, new kinematic quantities can be defined in a similar fashion as defined for
Fel. For example, the tensor
which is analogous to the elastic right Cauchy–Green deformation tensor Cel. As for the elastic part of the model, a free energy function
Wkin(
Cpl,e) is defined for the spring of the kinematic hardening contribution. Different stress tensors can be derived, for example
where 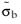 is a representation of the back stress in an intermediate frame defined by Fpl
is a representation of the back stress in an intermediate frame defined by Fpl. The yield function in
Equation 3-63 is defined in the spatial frame for large strains, thus to complete the formulation we need to define
σb or
Cple, which depends on the kinematic hardening model used.
For linear elastic materials, it is assumed that Wkin has the same form as the elastic strain energy function, and that it is always isotropic. Hence, for a linear elastic material the free energy function
Wkin reads
where εple = 0.5(
Cple−1) and
Ck is the kinematic hardening modulus.
The flow rule suggested for the Multiplicative Decomposition leads to an arbitrary plastic rotation, which is undesirable with the above formulation for kinematic hardening. Hence, when kinematic hardening is used, the plastic flow rule is modified to
where γk is a kinematic hardening parameter. The actual unknown used by the plasticity algorithm is the symmetric part of the inverse of
Fplv.
Conceptually, each branch corresponds to a spring and a dashpot in series, and all the branches are connected in parallel. The first branch always corresponds to linear kinematic hardening such that Fplv,1 = 1. Each consecutive branch adds an Armstrong–Frederick kinematic hardening model, where
Fplv,i is an additional variable with its own flow rule. The total back stress is then the sum of the stress in all branches
Both Isotropic Hardening and
Kinematic Hardening can be incorporated into the same plasticity model, a formulation known as
mixed hardening. These more refined hardening models are often necessary to accurately capture the true behavior of many materials.
where σe is the scalar equivalent stress.



