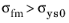A key concept for porous plasticity models is the evolution of the relative density, which is the solid volume fraction in a porous material. The relative density is related to the porosity (or void volume fraction) ϕ by

Shima and Oyane (Ref. 98) proposed a yield surface for modeling the compaction of porous metallic structures fabricated by sintering. The criterion can be applied for powder compaction at both low and high temperatures. The yield function and associated plastic potential is defined by an ellipsoid in the stress space. The plastic potential Qp is written in terms of both von Mises equivalent stress and mean pressure, and it also considers isotropic hardening due to changes in porosity. The plastic potential is defined by

where σe is the equivalent stress, σys0 is the initial yield stress, pm is the pressure, and ρrel is the relative density. The material parameters α, γ, and m are obtained from curve fitting experimental data. Typical material parameter values for copper aggregates are α = 6.2, γ = 1.03, and m = 5.

The Gurson criterion (Ref. 99) consists in a pressure-dependent yield function to describe the constitutive response of porous metals. The yield function is derived from the analytical expression of an isolated void immersed in a continuum medium. The void volume fraction, or porosity ϕ, is chosen as main variable.

In Gurson’s model, the yield function and associated plastic potential is not an ellipse in the stress space, as in the Shima–Oyane Criterion, but it is defined in terms of the hyperbolic cosine function. The plastic potential for the Gurson criterion reads

here, σe is the equivalent stress, σys0 is the initial yield stress, pm is the pressure, and ϕ is the porosity.

Tvergaard and Needleman modified the Gurson Criterion for porous plasticity to include parameters to better fit experimental data (Ref. 100-101). The resulting criterion is called the Gurson–Tvergaard–Needleman (GTN) criterion in the literature. The plastic potential for the GTN criterion reads

here, σe is the equivalent stress, σys0 is the initial yield stress, pm is the pressure, and ϕe is the effective void volume fraction (effective porosity). Typical correction parameter values are q1 = 1.5, q2 = 1.03, and q3 = q12.

The effective void value fraction (or effective porosity) ϕe used in the plastic potential is a function of the current porosity ϕ and other material parameters. It is often given by a bilinear function

where ϕc is the critical void volume fraction (critical porosity) at which void coalescence begins, and ϕf is the void volume fraction at failure.

When the porosity increases up to the value of failure, ϕf, the effective porosity takes a maximum value of ϕm and the porous material loses the capacity to carry stresses. The maximum porosity value is derived from other parameters

Since typical values for the parameters are q3 = q12, the maximum porosity value is given by ϕm = 1/q1.

A similar definition for ϕe that gives a smooth response as the material reaches failure is suggested in Ref. 103. It is based on a modification such that the effective void volume fraction reaches its maximum value asymptotically

The Fleck–Kuhn–McMeeking criterion (Ref. 104), also called the FKM criterion, was developed to model the plastic yielding of metal aggregates of high porosity. The yield function and associated plastic potential is derived for randomly distributed particles. The criterion is considered relevant for aggregates with porosity between 10% and 35%. The plastic potential for the FKM criterion reads

here, σe is the equivalent stress and pm is the pressure. The flow strength of the material under hydrostatic loading, pf, is computed from

here, σys0 is the initial yield stress, and ϕ is the void volume fraction (porosity). The maximum void volume fraction ϕm typically takes the value of 36%, the limit of dense random packing of sintered powder.

The FKM–GTN criterion is a combination of the Fleck–Kuhn–McMeeking Criterion and the Gurson–Tvergaard–Needleman Criterion, intended to cover a wider range of porosities (Ref. 105–106). The GTN model is used for low void volume fractions (porosity lower than 10%), and for void volume fractions higher than 25%, the FKM criterion is used. In the transition zone, a linear combination of both criteria is used.

See the sections Drucker–Prager Criterion and Compression Cap for details.

Since the relative density is related to the porosity ϕ by ρrel = 1 − ϕ, the change in porosity is also controlled by the change in plastic volumetric strain

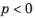
here, εN is the mean strain for nucleation, fN is the void volume fraction for nucleating particles, and sN is the standard deviation. Typical values for these parameters are εN = 0.04, sN = 0.1, and fN = 0.04. It is assumed that nucleation appears only in tension, and that there is no nucleation in compression.

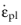
here, kw is a material parameter, ϕ is the current porosity, nD is a deviatoric tensor coaxial to the stress tensor, and is the plastic strain rate, which depends on the porous plasticity model. The weight w is computed from the Invariants of the Stress Tensor as

where θ is the Lode angle.

The variable w has a value of w = 0 at the compressive and tensile meridians (θ = 0 and θ = π/3), and it attains its maximum value, w = 1, for θ = π/6, which corresponds to maximum shear.

depends on the initial yield stress σys0, the hardening function σh, and the equivalent plastic strain in the porous matrix εpm.

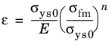It is also possible to include a power law relation between the equivalent plastic strain in the porous matrix εpm, and the flow stress (yield level) σfm. For uniaxial loading, the strain stress relation is written as (ref. Ref. 101)

where σys0 is the initial yield stress, n is the hardening exponent, and the Young’s modulus E is taken from the elastic material properties.

By writing the onset of plasticity as ε0 = σys0/E, and noting that ε = ε0 + εpm for σfm > σys0, this reads

which is equivalent to Swift isotropic hardening