where m(
x)
is the mean function and
f(
x) is a GP with zero mean and covariance
kθ(
x, x'). Here,
θ represents the hyperparameters of the covariance function.
where f = y − m(
x),
y is the evaluated QoI, and
f' and
x' are the predicted QoI and its corresponding input parameters.
where μ(
x)
and
cov(
x, x')
are the mean and covariance of the model, respectively:
Here, 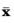 is defined as
is defined as 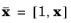 and ∑ = diag(σ02, σ2)
and ∑ = diag(σ02, σ2), where
σ0 and
σ = (σ1, …, σm) are the hyperparameters.
Further details about the covariance function and the Gaussian process can be found in
Ref. 7.
The covariance functions are assumed to be anisotropic. The automatic relevance determination (ARD) method is used to define different length scales for each input parameter. The ARD method is given its name because estimating the length scale parameters implicitly determines the “relevance” of each dimension. Input dimensions with relatively large length scales imply relatively little variation along those dimensions in the QoI function being modeled.
The spectral exponential kernel has strong smoothness where the Matérn kernel with ν = 5/2 is less smooth, and the Matérn kernel with
ν = 3/2 is more rough. The GP model with a spectral exponential kernel is infinitely differentiable, whereas the GP model with a Matérn kernel is differentiable a finite number of times. Comparing the Matérn kernel and a spectral exponential kernel with the same length scale, the Matérn kernel has weaker correlation and is more oscillatory. Samples from a GP with the one-layer neural network kernel can be viewed as superpositions of functions with a single-layer neural network with
erf(xT ∑ x') as the activation function. The GP model created with a single-layer neural network is smooth. In the region with a large absolute value of
x, they approximate to a constant value.
If there is a priori information of the mean function, it can be used to increase the modeling accuracy. One example of using a mean function is that when a GP is used for sensitivity analysis and uncertainty propagation, the extrapolation of the GP far from the sample points might be computed. If there is
a priori information of the mean, using a linear or quadratic mean function can be beneficial for the extrapolation.