where f(
x) is the probability density function for the input parameters
x, and the integration is performed over the region where the condition
COND(y,
z) is satisfied. Here,
y is the vector of the QoIs, and
z is the value of the threshold corresponding to each QoI.
For the jth QoI, the probability condition
cond(yj, zj) is true if
yj > zj or
yj < zj.
where n is the number of QoIs. In general, this integration is impossible to obtain with analytical methods.
The expected feasibility function (EFF), which is used as the adaptive error estimation in EGRA, is used to select the location of the next input parameter point. The EFF defines the expectation of the sample lying within the vicinity, defined by ±ε(x), around the limit state. The feasibility function at
x is defined as being positive within the vicinity around the limit state and 0 otherwise. For problems with a scalar value QoI
y, the EFF is defined as the expectation of being within the vicinity around the limit state given by
where 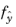 is the probability of the AGP and y
is the probability of the AGP and y is realizations of
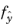
. Note that
ε defines the vicinity around
z and is set to
2σy, where
σy is the standard deviation of the AGP model.
Here, Nf is the number of predicted QoIs that satisfy the criteria, and
N is the number of all samples. One drawback of this method is that the majority of the samples lie in the high-probability region of the input parameter space. If the region defined by the threshold is a low-probability region, a very large number of samples is required to ensure enough samples to be located in such a region. Another method is the multimodal adaptive importance sampling method, which combines the surrogate model and Latin hypercube sampling. Compared to the Latin hypercube method, the importance sampling method uses fewer samples and provides an error estimation.