You are viewing the documentation for an older COMSOL version. The latest version is
available here.
|
|
In the literature, the terms viscoplasticity and creep are often used interchangeably to refer to the class of problems related to rate-dependent plasticity. A distinction is sometimes made so that creep refers to models without a yield surface.
|
|
•
|
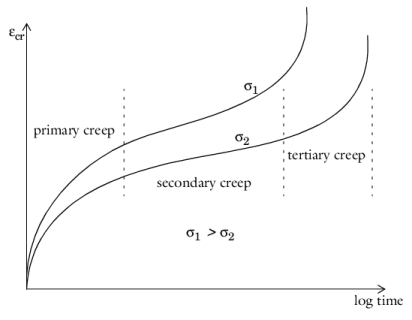
In the initial primary creep regime (also called transient creep) the creep strain rate decreases with time to a minimum steady-state value.
|
|
•
|
In the secondary creep regime the creep strain rate is almost constant. This is also called steady-state creep.
|
|
•
|
In the tertiary creep regime the creep strain increases with time until a failure occurs.
|
In most cases, Fcr1 and
Fcr3 depend on stress, temperature, and time, while secondary creep,
Fcr2, depends only on stress level and temperature. Normally, secondary creep is the dominant process. Tertiary creep is seldom important because it only accounts for a small fraction of the total lifetime of a structure or mechanical component.
where λcr is the creep multiplier,
Qcr is the creep potential, and
σ is the stress tensor. The creep multiplier is an explicit function of stress
σ, temperature
T, time
t, and the equivalent creep strain
εce, and can be given on a general format as
where the generic functions f,
g, and
h that define the creep rate and can be combined to construct different types of creep models. The hardening rule,
h(εce,
t), defines the relationship between the creep strain tensor
εcr and the equivalent creep strain
εce. The equivalent stress
σe is a scalar representation of the Cauchy stress tensor, and given associative creep flow, it also defines the creep potential so that
The creep rate function f is typically a function of the equivalent stress
σe or any other scalar measure of the current stress state. In COMSOL Multiphysics, there are several built-in creep rate functions:
It is also possible to define an arbitrary expression for f so that, in principle, any creep model can be implemented. The expressions used for the built-in creep rate functions are described in the following sections.
The Norton model is the most common secondary creep model, where the creep rate is assumed proportional to a power law of the equivalent stress
σe such that
(3-130)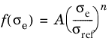
where A is the creep rate coefficient,
n is the stress exponent,
σref is a reference stress level.
At very high stress levels the creep rate is proportional to the exponential of σe. Garofalo showed (
Ref. 8,
Ref. 9) that the power-law and exponential creep are limiting cases for the general empirical expression
This equation reduces to a power-law (the Norton model) when ασe < 0.8 and approaches exponential creep for
ασe > 1.2, where 1
/α is a reference equivalent stress level. The
Garofalo (Hyperbolic sine law) creep model implemented in COMSOL Multiphysics is given as
For metals at low stress levels and high temperatures, Nabarro and Herring (Ref. 6,
Ref. 7) independently derived an expression for the creep rate as a function of atomic diffusion, so called diffusional creep. The
Nabarro–Herring model implemented in COMSOL Multiphysics is given as
where d is the grain diameter,
Dv is the volume diffusivity through the grain interior,
b is the Burgers vector,
kB is the Boltzmann’s constant,
T is the absolute temperature.
Another model for diffusional creep is the Coble creep model (
Ref. 6,
Ref. 7), which is closely related to Nabarro–Herring creep, but takes into account the grain boundary diffusivity through the parameter
Dgb. The
Coble creep model implemented in COMSOL Multiphysics is given as
Generally, the stress exponent n in the Weertman model takes a value between 3 and 5 when modeling dislocational creep.
where J2 is the second invariant of the stress deviator. If creep is orthotropic, the
Hill orthotropic equivalent stress can be used, which is given by
(3-131)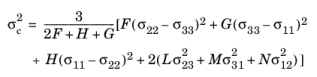
where F,
G,
H,
L,
M, and
N are Hill’s coefficients that relate the anisotropy to the local coordinates. In the above equation it is assumed that an average equivalent stress can be computed from
F,
G, and
H using a von Mises like expression; this assumption leads to the first term on the right-hand-side of
Equation 3-131.
The dimensionless tensor N, which gives the direction of the creep flow, is computed from the creep potential
Qcr as
When von Mises equivalent stress is used, the potential equals Qcr = σmises, and the deviatoric tensor
Ndev is defined as done for
J2 plasticity (see
Isotropic Plasticity)
(3-132)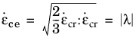
The same hardening rule is also used when the Hill orthotropic equivalent stress is selected.
For the Pressure equivalent stress, the flow direction is volumetric
The creep hardening function h is typically a function of time
t and the equivalent creep strain
εce. In COMSOL Multiphysics, there are two built-in hardening functions,
Strain hardening and
Time hardening, and it is also possible to specify a user defined expression. Also, it is possible to add hardening to any of the built-in creep models.
where the time hardening function is given by the power law
here, tshift is a time shift,
tref is a reference time, and
m is the hardening exponent.
Similarly, the strain hardening function is given by the power law
where εshift is the equivalent creep strain shift,
tref is a reference time, and
m is the hardening exponent.
The strain shift εshift and the time shift
tshift in the hardening functions serve two purposes:
The temperature shift function g typically depends on the absolute temperature
T. In COMSOL Multiphysics, an
Arrhenius temperature function is built-in, but it is also possible to specify a user defined expression.
The Arrhenius temperature function is given as
where Q is the activation energy (J/mol),
R is the gas constant,
T is the absolute temperature, and
Tref is a reference temperature.
Using a combination of f,
g, and
h together with the definition of the equivalent stress
σe makes it possible to construct sophisticate creep models. For example, the often used temperature-dependent isotropic Norton creep model is obtained by the following settings:
Several creep rate contributions can be added to the total creep rate to construct more elaborate models. This is done by adding one or more Additional Creep subnodes to an existing
Creep node. There are no restrictions on how to combine models; for example, a
von Mises based creep flow contribution can be combined with a
Pressure based creep flow contribution.
|
|
|
•
|
In the example Combining Creep Material Models: Application Library path Nonlinear_Structural_Materials_Module/Creep/combined_creep a Norton–Bailey model for primary creep is combined with a Norton model for secondary creep. Both creep models are temperature dependent. The resulting creep-rate equation becomes
|
|
(3-133)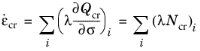
(3-134)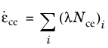
where Ncr and
Nce are tensors that describe the direction of
εcr and
εce, respectively.
The Backward Euler method is used to discretize these equations as
(3-135)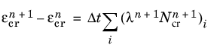
(3-136)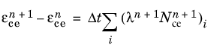
where n+1 indicates that the variable is evaluated at the current time step, and
Δt is the time step. The creep strain tensor
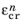
and equivalent creep strain
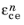
at the previous time step are stored as internal state variables.
Equation 3-135 and
Equation 3-136 define a system of nonlinear equations that is solved locally at each Gauss point for
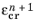
and
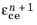
using Newton’s method.
The Forward Euler method is used to discretize
Equation 3-133 and
Equation 3-134 as
(3-137)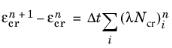
(3-138)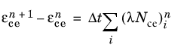
such that all quantities on the right-hand-side are evaluated at the previous time step. This means that Equation 3-137 and
Equation 3-138 define an explicit update of
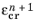
and
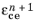
given only known quantities from the previous time step. The forward Euler method is only conditionally stable, and the time step of the global time marching scheme has to be constrained to preserve stability and accuracy of the method. In COMSOL Multiphysics the limit for a stable time step is estimated as
where εel is the elastic strain tensor. This estimate in principle restricts the creep increment to be smaller than the current state of stress, and
1/4 is a constant to make the estimate conservative. The final value is computed as the minimum value over all Gauss points in the domain where the creep feature is active.
For Domain ODEs,
Equation 3-133 and
Equation 3-134 are converted to weak-form and solved as part of the general initial-boundary value problem. The components of the creep strain tensor
εcr and the equivalent creep strain
εce are then treated as degrees-of-freedom.
The equations described in the previous sections about the different creep models differ from the forms most commonly found in the literature. The main difference lies in the introduction of normalizing reference values such as the reference stress σref and reference time t
ref. These values are in a sense superfluous and can in principle be chosen arbitrarily. The choice of reference values, however, affects the numerical values to be entered for the material data. The implementation in COMSOL Multiphysics has two advantages:
The coefficient AN has a physical dimension that depends on the value of
n, and the unit has an implicit dependence on the stress and time units. Converting the data to the format used in COMSOL Multiphysics (for example,
Equation 3-130) requires the introduction of the reference stress
σref. It is convenient here to use the implicit stress unit for which
AN is given as the reference stress. The creep rate coefficient
A will then have the same numerical value as
AN, and you do not need to do any conversions.
The physical dimension of A is, however, (time)
−1, whereas the physical dimension of
AN is (stress)
−n(time)
−1.
Another popular way of representing creep data is to supply the stress giving a certain creep rate. As an example, σc7 is the stress at which the creep strain rate is
10−7/h. Data on this form is also easy to enter: You set the reference stress
σref to the value of
σc7 and enter the creep rate coefficient
A as
1e-7[1/h].
|
•
|
σc7 = 70 MPa, and stress exponent n = 4.5.
|
|
•
|
AN = 4.98 ·10-16 with respect to units MPa and hours, and stress exponent n = 4.5.
|
Since the stress inside in the Garofalo law appears as an argument to a sinh() function, it must necessarily be dimensionless. Most commonly this is however written as
Viscoplasticity, as well as Creep, is an inelastic time-dependent deformation that occurs when the material is subjected to stress (typically much less than the yield stress). The growth of unrecoverable strains depend on the rate at which loads are applied, effect that is normally enhanced by high temperatures.
The viscoplastic strain εvp is computed by a flow rule that defines the relationship between the rate of
εvp and the current state of stress and temperature.
When an associative flow and von Mises equivalent stress σe are used, so
Qvp = σe, the rate of
εvp is coaxial to the stress deviator and the viscoplastic flow rule is written as
where Qvp is the viscoplastic potential,
σ is the stress tensor, and
Ndev = ∂Qvp / ∂σ is the flow direction.
The viscoplastic multiplier λvp depicts a different expression for different viscoplastic models (Anand, Chaboche, and so on), and it is equal to the equivalent viscoplastic strain rate
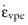
Setting different measures for the equivalent stress σe (von Mises, Tresca, Hill) allows to define different viscoplastic multiplier and flow directions, see
Equivalent Stress, Creep Flow and Hardening Rule for details.
Anand viscoplasticity (Ref. 9) is a deviatoric viscoplastic model suitable for isotropic viscoplastic deformations. As for the models described in
Creep, the Anand model has no yield surface.
The rate of εvp is determined by the viscoplastic multiplier
λvp which is a function of stress
σ and temperature
T, and it is given by
here, A is the viscoplastic rate coefficient,
Q is the activation energy (J/mol),
ξ is the stress multiplier,
m is the stress sensitivity, and
R is the gas constant.
The deformation resistance, sa (SI unit: Pa), controls the hardening behavior of the Anand model. In COMSOL Multiphysics it is derived for the normalized
resistance factor, sf, and the
deformation resistance saturation coefficient,
ssat, such that
sa =
ssat sf. The resistance factor
sf is a dimensionless internal variable that is computed by the evolution equation
with the initial condition sf(0) = sinit /
ssat. The evolution of the resistance factor
sf is controlled by the dimensionless hardening function
were h0 (SI unit: Pa) represents a constant rate of
athermal hardening in the curve stress versus strain (
Ref. 9). The use of the sign function and the absolute value in the hardening function permits the modeling of either strain hardening or strain softening, depending on whether
sf is greater or smaller than the saturation value
sf*.
The saturation value sf* is calculated from the expression
where n is the
deformation resistance sensitivity exponent.
Anand–Narayan model (Ref. 10) is suitable for modeling the viscoplastic deformation of lithium.
where A is the viscoplastic rate coefficient,
Q is the activation energy (J/mol),
ξ is the stress multiplier,
m is the stress sensitivity, and
R is the gas constant.
The deformation resistance, sa (SI unit: Pa), is computed with an extra dependent variable as done for
Anand Model.
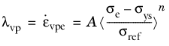 for
for 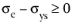
Here, A is the viscoplastic rate coefficient (SI unit: 1/s),
n is the stress exponent (dimensionless), and
σref is a reference stress level (SI unit: Pa).
The Macaulay brackets < • > are applied on the yield function, which is defined as done for plasticity
The equivalent stress σe is either the von Mises, Tresca, or Hill orthotropic stress, or a user defined expression; and
σys is the yield stress (which may include an
Numerical Solution of the Elastoplastic Conditions model). The stress tensor used in the equivalent stress
σe is shifted by what is usually called the
back stress,
σback when
Kinematic Hardening is included.
The deviatoric tensor Ndev is computed from the viscoplastic potential
Qvp
When von Mises equivalent stress is used, the associated flow rule reads Qvp = F, and the deviatoric tensor
Ndev is defined as done for deviatoric creep.
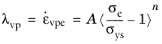 for
for 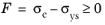
As described for Chaboche Model, the equivalent stress
σe can be either von Mises (default), Tresca, Hill orthotropic stress, or a user defined expression. The flow direction
Ndev = ∂Qvp / ∂σ is computed from the viscoplastic potential
Qvp, which can be associated or nonassociated.
Bingham model is equivalent to Chaboche Model when setting the exponent
n = 1, and denoting the viscosity as the quotient
η = σref/
A. The equivalent viscoplastic strain rate (viscoplastic multiplier) is given by
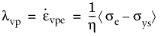 for
for 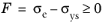
As described for Chaboche Model, the equivalent stress
σe can be either von Mises (default), Tresca, Hill orthotropic stress, or a user defined expression. The flow direction
Ndev = ∂Qvp / ∂σ is computed from the viscoplastic potential
Qvp, which can be associated or nonassociated.
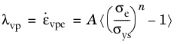 for
for 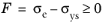
As described for Chaboche Model, the equivalent stress
σe can be either von Mises (default), Tresca, Hill orthotropic stress, or a user defined expression. The flow direction
Ndev = ∂Qvp / ∂σ is computed from the viscoplastic potential
Qvp, which can be associated or nonassociated.
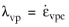 for
for 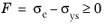
The conditional evaluation F ≥ 0 is handled automatically.
By default, an associative flow and von Mises equivalent stress σe are used, so
Qvp = F, the rate of
εvp is coaxial to the stress deviator, and the viscoplastic flow rule is written as
The temperature function g typically depends on the absolute temperature
T. In COMSOL Multiphysics, an
Arrhenius temperature function is built-in, but it is also possible to specify a user defined expression.
The Arrhenius temperature function is given as
where Q is the activation energy (J/mol),
R is the gas constant,
T is the absolute temperature, and
Tref is a reference temperature.
The rate equations given by the viscoplastic flow rule and evolution equations for the two internal variables are integrated in time to compute the value of the viscoplastic strain tensor εvp, the equivalent creep strain
εvpe, and other possible internal variables (for instance, the resistance factor
sf in Anand model) at each time step. This can be done using any of the following methods:
The Backward Euler method is used to discretize these equations as
(3-139)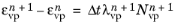
(3-140)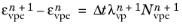
where Nvp and
Nvpe are tensors that describe the direction of
εvp and
εvpe, respectively,
n+1 indicates that the variable is evaluated at the current time step, and
Δt is the time step.
For Anand Model an extra equation is solved for the
resistance factor, sf,
(3-141)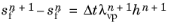
For Domain ODEs, the evolution equations of the viscoplastic model are converted to weak-form and solved as part of the general initial-boundary value problem. The components of
εvp,
εvpe, and
sf are then treated as degrees of freedom.
When the Large strains formulation is selected in the
Creep or
Viscoplasticity nodes, a
Multiplicative Decomposition of deformation gradients is used
here, F is the deformation gradient,
Fel is the elastic deformation, and
Fin is inelastic deformation due to creep or viscoplasticity.
(3-142)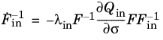
where λin is the equivalent creep or viscoplastic strain rate, and
Qin is the creep or viscoplastic potential. For creep and viscoplasticity in metals (so-called
J2 plasticity) the viscoplastic potential depends on the deviatoric stress,
Qin = Qin(J2 (σ)), and the flow direction is deviatoric,
Ndev = ∂Qin / ∂σ.
For large strains, Equation 3-142 is numerically solved with the so-called
exponential mapping technique, as described in
Numerical Solution of the Elastoplastic Conditions, and the elastic deformation gradient then obtained from
The Bergstrom–Boyce model (Ref. 35–
36) is a viscoplastic material that successfully capture such phenomena, and it is suitable for modeling rubbers and elastomers.
The stiffness in the spring is defined by the energy factor βv. This factor multiplies the isochoric strain energy density defined in the main hyperelastic branch, in a similar way as done for
Large Strain Viscoelasticity. For instance, if the main branch is defined by an
Arruda–Boyce hyperelastic material with a shear modulus
μ0, then the shear modulus in the spring is
μ1 = βvμ0.
here, F is the deformation gradient in the hyperelastic branch,
Fel is the elastic deformation in the spring, and
Fvp is inelastic deformation in the dashpot.
The viscoplastic velocity gradient, Lvp, is energy conjugate to the stress tensor
σ in the branch. For volume-preserving viscoplasticity, it is defined as
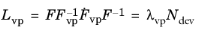 with
with 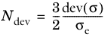
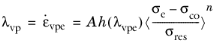 for
for 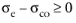
here, A is the viscoplastic rate coefficient,
σe is the von Mises stress in the network,
σco is a cutoff stress,
σres is the flow resistance, and
n is the stress exponent.
The strain hardening function h(λvpe) is defined by the power-law
Here, c is the strain hardening exponent and
ξ is a small numerical constant. The equivalent viscoplastic stretch
λvpe is computed from the viscoplastic deformation
The Bergstrom–Bischoff model, also known as the three network model (
Ref. 35,
Ref. 37) is suitable for modeling elastomers and thermoplastics. The rheology is similar to the Bergstrom–Boyce model, but it adds two parallel branches instead of one.
The stiffness in the spring in the first branch is defined by the energy factor βv1. This factor multiplies the isochoric strain energy density defined in the main hyperelastic branch, in a similar way as done for
Bergstrom–Boyce Model. For instance, if the main branch is defined by an
Arruda–Boyce hyperelastic material with a shear modulus
μ0, then the stiffness in the spring is
μ1 = βv1μ0.
here, A is the viscoplastic rate coefficient,
σe,1 is the von Mises stress in the branch,
σres,1 is the flow resistance,
a1 is a material parameter to control the influence of the hydrostatic stress, and
n1 is the stress exponent.
The energy factor in the second branch βv2 is computed after solving the rate equation
Here, βv2 is the final energy factor after saturation. The energy factor is initialized to a value equal to
βv2 = βvi. The energy factor
βv2 then multiplies the isochoric strain energy density defined in the main hyperelastic branch to define the stiffness of the spring in the second branch, in a similar way as done in the first branch.
here, σe,2 is the von Mises stress in the branch,
σres,2 is the flow resistance,
a2 is a material parameter to control the influence of the hydrostatic stress, and
n2 is the stress exponent.
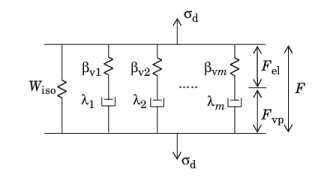
The Parallel Network model (Ref. 35,
Ref. 37) can be seen as a generalized version of the
Bergstrom–Boyce Model, where several viscoplastic branches can be added in parallel to the main hyperelastic branch.
For example, it is possible to combine a Neo-Hookean material in the main hyperelastic branch with two parallel spring-dashpot branches characterized by an
Arruda–Boyce model.
Several networks can be added to build more elaborate viscoplasticity models, and the energy factors βvi are used to differentiate the response of the additional stiffnesses. This is done by adding one or more
Additional Network subnodes to an existing
Polymer Viscoplasticity node. The rheological representation of this model can be seen in
Figure 3-29.
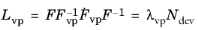 with
with 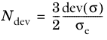
The temperature function g(
T) depends on the absolute temperature
T, and it acts as a multiplier for the viscoplastic rate.
The Arrhenius temperature function is given as
where Q is the activation energy (J/mol),
R is the gas constant,
T is the absolute temperature, and
Tref is a reference temperature.
The Power law temperature function is given as
where T is the absolute temperature,
Tref is a reference temperature, and
m is the temperature exponent.
|
|
When the Calculate dissipated energy check box is selected, the dissipation rate density due to creep is available under the variable solid.Wcdr and the dissipation rate density due to viscoplasticity is available under the variable solid.Wvpdr. The dissipated energy density due to creep is available under the variable solid.Wc and due to viscoplasticity under the variable solid.Wvp. Here solid denotes the name of the physics interface node.
|

