You are viewing the documentation for an older COMSOL version. The latest version is
available here.
where fc can be a constant value (for perfectly plastic materials), or a variable for strain-hardening materials. The yield surface
F is a surface in the space of principal stresses, in which the elastic regime (
F ≤ 0) is enclosed.
For brittle materials, the yield surface represents a failure surface, which is a stress level at which the material collapses instead of deforms plastically.
|
|
Some authors define the yield criterion as f ( σ) = fc, while the yield surface is an isosurface in the space of principal stresses F = 0, which can be chosen for numerical purposes as 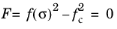 .
|
|
|
|
•
|
If the Include geometric nonlinearity check box is selected in Settings window of the study, the default is to use a multiplicative decomposition.
|
|
The flow rule defines the relationship between the increment of the plastic strain tensor
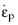
and the current state of stress,
σ, for a yielded material subject to further loading. The direction of the plastic flow is defined by
Here, λ is a positive multiplier (also called the
consistency parameter or
plastic multiplier), which depends on the current state of stress and the load history, and
Qp is the
plastic potential.
The plastic multiplier λ is determined by the
complementarity or
Kuhn–Tucker conditions
where Fy is the
yield function. The yield surface encloses the elastic region defined by
Fy <
0. Plastic flow occurs when
Fy =
0.
If the plastic potential and the yield surface coincide with each other (Qp =
Fy), the flow rule is called
associated, and the rate in
Equation 3-50 is solved together with the conditions in
Equation 3-49.
(3-50)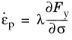
For a nonassociated flow rule, the yield function does not coincide with the plastic potential, and together with the conditions in
Equation 3-49, the rate in
Equation 3-51 is solved using the plastic potential
Qp (often, a smoothed version of
Fy).
(3-51)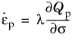
|
|
When additive plasticity is used and the Include geometric nonlinearity check box is selected on the study Settings window, the Cauchy stress tensor is used to evaluate the yield function and plastic potential. Plastic flow is, however, assumed in the direction the second Piola–Kirchhoff stress tensor, and the computed plastic strain tensor can be interpreted as a Green–Lagrange strain.
|
For a large strain formulation with multiplicative decomposition of deformation (Ref. 3,
Ref. 4, and
Ref. 5), the plastic flow rule can be written as the
Lie derivative of the elastic left Cauchy–Green deformation tensor
Bel:
(3-52)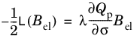
The plastic multiplier λ and the plastic potential
Qp (written in terms of the Cauchy stress tensor
σ) satisfy the Kuhn–Tucker condition, as done for infinitesimal strain plasticity
|
|
The yield function Fy in Ref. 3 and Ref. 4 was written in terms of Kirchhoff stress τ and not Cauchy stress σ because the authors defined the plastic dissipation with the conjugate energy pair τ and d, where d is the rate of strain tensor.
|
The Lie derivative of Bel is then written in terms of the plastic right Cauchy–Green rate
(3-53)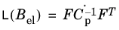
By using Equation 3-52 and
Equation 3-53, the plastic flow rule is written as (
Ref. 4)
(3-54)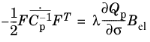
For the associated flow rule, the plastic potential and the yield surface coincide with each other (Qp =
Fy), and for the nonassociated case, the yield function does not coincide with the plastic potential.
(3-55)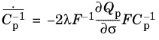
After integrating the flow rule in Equation 3-55, the plastic Green–Lagrange strain tensor is computed from the plastic deformation tensor
For isotropic plasticity, the plastic potential Qp is written in terms of at most three invariants of Cauchy’s stress tensor
(3-56)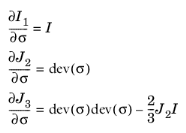
The trace of the incremental plastic strain tensor, which is called the volumetric plastic strain rate 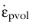
, is only a result of dependence of the plastic potential on the first invariant
I1(
σ), since
∂J2/∂σ and
∂J3/∂σ are deviatoric tensors
A common measure of inelastic deformation is the equivalent plastic strain rate, (or
equivalent von Mises strain rate) which is defined from the plastic shear components
(3-57)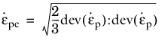
(3-58)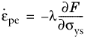
(3-59)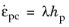
where σys is the yield stress. The scalar function
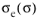
is called equivalent stress. The default form of the equivalent stress is the
von Mises stress, which is often used in metal plasticity:
Other expressions can be defined, such as Tresca stress,
Hill equivalent stress, or a user defined expression.
where σys is the
yield stress level (yield stress in uniaxial tension) and
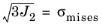
is the equivalent von Mises stress.
By using the representation of principal stresses in term of the invariants J2 and the Lode angle 0
≤ θ ≤ π/3, the Tresca criterion can alternatively be written as
The maximum shear stress is reached at the meridians (θ =
0 or
θ =
π/3). The Tresca criterion can be circumscribed by setting the Lode angle
θ =
0, or equivalently, by a von Mises criterion
The minimum shear is reached at θ =
π/6, so the Tresca criterion can be inscribed by setting a von Mises criterion
When dealing with soils, the parameter k is also called
undrained shear strength.
|
|
The Tresca equivalent stress, σtresca = σ1 − σ3, is implemented in the variable solid.tresca, where solid is the name of the physics interface node.
|
The von Mises and Tresca criteria are independent of the first stress invariant I1 and are mainly used for the analysis of plastic deformation in metals and ductile materials, though some researchers also use these criteria for describing fully saturated cohesive soils under undrained conditions. The von Mises and Tresca criteria belong to what researchers call
volume preserving or
J2 plasticity, as the plastic flow is independent on the mean pressure.
Hill (Ref. 6,
Ref. 7) proposed a quadratic yield function (and associated plastic potential) in a local coordinate system given by the principal axes of orthotropy
ai
(3-60)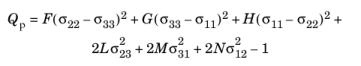
The six parameters F,
G,
H,
L,
M, and
N are related to the state of anisotropy. As with isotropic plasticity, the elastic region
Qp < 0 is bounded by the yield surface
Qp = 0.
|
|
Hill plasticity is an extension of J2 (von Mises) plasticity, in the sense that it is volume preserving. Due to this assumption, six parameters are needed to define orthotropic plasticity, as opposed to orthotropic elasticity, where nine elastic coefficients are needed.
|
Hill noticed that the parameters L,
M, and
N are related to the yield stress in shear with respect to the axes of orthotropy
ai, thus they are positive parameters
Here, σysij represents the yield stress in shear on the plane
ij.
The material parameters σys1,
σys2, and
σys3 represent the tensile yield stress in the direction,
a1,
a2, and
a3, and they are related to Hill’s parameters
F,
G, and
H as
(3-61)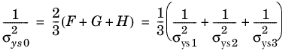
Defining Hill’s equivalent stress as (
Ref. 7)
now depends on the initial yield stress σys0, the hardening function
σh, and the equivalent plastic strain
εpe.
where the yield stress σys(εpe) is a function of the
equivalent plastic strain εpe.
In the settings for plasticity you specify the equivalent stress σe(σ) for the yield function; and
σys0 that defines the onset of plastic deformation.
The yield stress σys(εpe) is for linear isotropic hardening a function of the
equivalent plastic strain εpe and the
initial yield stress σys0
Here, the isotropic hardening modulus Eiso is calculated from
For linear isotropic hardening, the isotropic tangent modulus ETiso is defined as (stress increment / total strain increment). A value for
ETiso is entered in the isotropic tangent modulus section for the Plasticity node. The Young’s modulus
E is taken from the parent material (Linear Elastic, Nonlinear Elastic or Hyperelastic material model). For orthotropic and anisotropic elastic materials,
E represents an equivalent Young’s modulus.
In the Ludwik model for nonlinear isotropic hardening, the yield stress σys(εpe) is defined by a nonlinear function of the equivalent plastic strain. The Ludwik equation (also called the Ludwik–Hollomon equation) for isotropic hardening is given by the power law
Here, k is the strength coefficient and
n is the hardening exponent. Setting
n = 1 would result in linear isotropic hardening.
Similar to the Ludwik hardening model, the yield stress σys(εpe) in the Johnson–Cook model is defined as a nonlinear function of the equivalent plastic strain
εpe given by a power law. The difference is that effects of the strain rate are included in the model. The yield stress and hardening function is given by
(3-62)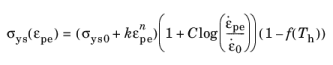
The Johnson–Cook model also adds the possibility to include thermal softening by including a function which depends on the normalized homologous temperature Th. It is a function of the current temperature
T, the melting temperature of the metal
Tm, and a reference temperature
Tref
The strain rate strength coefficient C and the reference strain rate
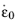
in the Johnson–Cook model are obtained from experimental data. The flow curve properties are normally investigated by conducting uniaxial tension tests in a temperature range around half the melting temperature
Tm, and subjected to different strain rates like 0.1/s, 1/s, and 10/s.
It should be noted that the intent of the strain rate dependent term in Equation 3-62 is to capture the hardening at high strain rates. If extrapolated to very low strain rates, a low or even negative yield stress will be predicted. Low strain rates can however be expected in some regions in a general finite element model. To resolve this, the material model as implemented, never evaluates the logarithmic term to a value smaller than zero. This means that the reference strain rate
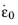
must be considered the quasistatic limit. Below this strain rate, the hardening function will be a strain rate independent, but temperature dependent, Ludwik law:
here, k is the strength coefficient,
n is the hardening exponent, and
ε0 is a reference strain. Noting that at zero plastic strain the initial yield stress is related to the strength coefficient and hardening exponent as
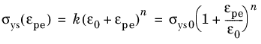 for
for 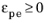
The yield stress σys(εpe) is then defined as
The value of the saturation exponent parameter
β determines the saturation rate of the hysteresis loop for cyclic loading. The
saturation flow stress σsat characterizes the maximum distance by which the yield surface can expand in the stress space. For values
εpe >> 1/β, the yield stress saturates to
where σ∝ is the
steady-state flow stress,
m the saturation coefficient and
n the saturation exponent. For values
mεpen >> 1 the yield stress saturates to
(3-63)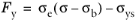
Here, σys is the yield stress (which may include a linear or nonlinear isotropic hardening model), and
σe (σ) is the equivalent stress. The stress tensor used in the yield function is shifted by what is usually called the
back stress,
σb to impose kinematic hardening.
where the kinematic hardening modulus Ck is calculated from
The value for Ek is entered in the
kinematic tangent modulus section and the Young’s modulus
E is taken from the linear or nonlinear elastic material model. For orthotropic and anisotropic elastic materials,
E represents an averaged Young’s modulus. Note that some authors define the kinematic hardening modulus as
Hk = 2/3Ck.
Armstrong and Frederick (Ref. 1) added memory to Prager’s linear kinematic hardening model. This nonlinear kinematic hardening model makes it possible to capture the Bauschinger effect and nonlinear behavior by nonsymmetric tension-compression loading.
here, Ck is the kinematic hardening modulus,
γk is a kinematic hardening parameter, and
εpe the equivalent plastic strain. Setting
γk = 0 recovers Prager’s rule for linear kinematic hardening.
Chaboche (Ref. 2) proposed a nonlinear kinematic hardening model based on the superposition of
N back stress tensors
each of these back stress tensors σb,i follows a nonlinear Armstrong–Frederick kinematic hardening rule
(3-64)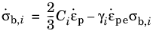
Practitioners would normally select γk = 0 for one of the back stress equations, thus recovering Prager’s linear rule for that branch
The back stress tensor σb is then defined by the superposition of
N back stress tensors
For multiplicative decomposition, the total deformation gradient F is decomposed into an elastic
Fel and an inelastic (plastic)
Fpl deformation
as described in Inelastic Strain Contributions. When kinematic hardening is used with multiplicative decomposition,
Fpl is similarly split multiplicatively as suggested in
Ref. 8, such that
Here Fple is referred to as the “elastic” part of
Fpl, and
Fplv as its “viscous” part of the plastic deformation. Conceptually,
Fple corresponds to a spring and
Fplv to a dashpot that are connect in series in a rheological model. Now new kinematic quantities can be defined in a similar fashion as for
Fel. For example, the tensor
which is analogous to the elastic right Cauchy–Green deformation tensor Cel. As for the elastic part of the model, a free energy function
Wkin(
Cpl,e) can be defined for the spring of the kinematic hardening part. From
Wkin different stress tensors can be derived, for example
where 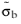 is a representation of the back stress in an intermediate frame defined by Fpl
is a representation of the back stress in an intermediate frame defined by Fpl. The yield function in
Equation 3-63 is defined in the spatial frame for large strains, thus to complete the formulation we need to find
σb, or
Cple, which depends on the kinematic hardening model used.
It is in COMSOL Multiphysics assumed that Wkin has the same format as the elastic strain energy function and that it is always isotropic. Hence for a linear elastic material
where εple = 0.5(
Cple-1) and
Ck is the kinematic hardening modulus. For hyperelastic materials, a compressible Neo-Hookean strain energy function is used
The flow rule suggested in Plastic Flow for Multiplicative Decomposition leads to an arbitrary plastic rotation, which is undesirable with the above formulation for large strain kinematic hardening. Hence, when kinematic hardening is used, the plastic flow rule is modified to
where γk is a kinematic hardening parameter. The actual unknown used by the plasticity algorithm is the symmetric part of the inverse of
Fplv.
Conceptually, each branch corresponds to a spring and a dashpot in series and the branches are then connected parallel. The first branch always corresponds to linear kinematic hardening such that Fplv,1 = 1. Each consecutive branch adds an Armstrong–Frederick kinematic hardening model, where
Fplv,i is an additional unknown with its own flow rule. The total back stress is then the sum of the stress in all branches
here, τ is the shear stress,
c the cohesion, and
ϕ denotes the angle of internal friction.
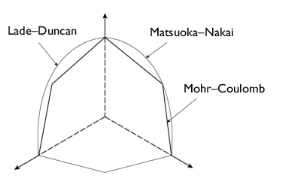
The Mohr–Coulomb criterion can be written in terms of the invariants I1 and
J2 and the Lode angle 0
≤ θ ≤ π/3 (
Ref. 1,
Ref. 11) when the principal stresses are sorted as
σ1 ≥ σ2 ≥ σ3. The yield function then reads
The tensile meridian is defined when θ =
0 and the compressive meridian when
θ =
π/3.
In the special case of frictionless material, (ϕ =
0,
α =
0,
k =
c), the Mohr–Coulomb criterion reduces to a Tresca’s maximum shear stress criterion,
(σ1 − σ3) =
2k or equivalently
The Mohr–Coulomb criterion causes numerical difficulties when treating the plastic flow at the corners of the yield surface. The Drucker–Prager model (Ref. 1,
Ref. 2) neglects the influence of the invariant
J3 (introduced by the Lode angle) on the cross-sectional shape of the yield surface. It can be considered as the first attempt to approximate the Mohr–Coulomb criterion by a smooth function based on the invariants
I1 and
J2 together with two material constants (which can be related to Mohr–Coulomb’s coefficients)
The coefficients in the Drucker–Prager model are related to the cohesion c and angle of internal friction
ϕ in the Mohr–Coulomb criterion by the relation
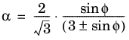 and
and 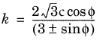
In the special case of frictionless material, (ϕ =
0,
α =
0,
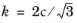
), the Drucker–Prager criterion reduces to the von Mises criterion
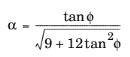 and
and 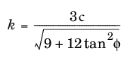
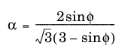 and
and 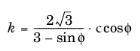
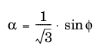 and
and 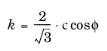
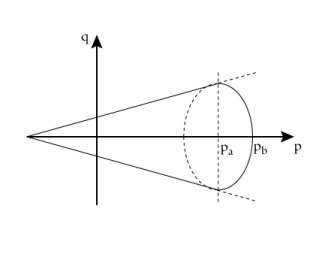
The elliptic cap is an elliptic yield surface of semi-axes as shown in Figure 3-19. The initial pressure
pa (SI units: Pa) denotes the pressure at which the elastic range circumscribed by either a Mohr–Coulomb pyramid or a Drucker–Prager cone is not valid any longer, so a cap surface is added. The limit pressure
pb gives the curvature of the ellipse, and denotes the maximum admissible hydrostatic pressure for which the material starts deforming plastically. Pressures higher than
pb are not allowed.
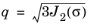 and
and 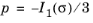
the point (pa,
qa) in the Haigh–Westergaard coordinate system is where the elliptic cap intersects either the Mohr–Coulomb or the Drucker–Prager cone.
where Ia = −3pa,
Ib = −3pb, and
Ja is the ellipse semiaxis in the
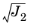 − I1
− I1 plane, given by the intersection with the Drucker–Prager criterion
here, pb0 is the initial value for the limit pressure
pb,
Kiso is the isotropic hardening modulus,
εpvol the volumetric plastic strain, and
εpvol,max the maximum volumetric plastic strain. The volumetric plastic strain
εpvol is negative in compression, so the limit pressure
pb is increased from
pb0 as hardening evolves.
Instead of providing the value for the initial pressure pa (SI units: Pa), the ellipse’s aspect ratio
R is entered. The ellipse aspect ratio
R is given by
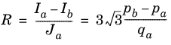 where
where 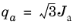
The ellipse semiaxis in the 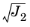 − I1
− I1 plane is given by the aspect ratio
R
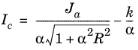 and
and 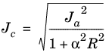
Matsuoka and Nakai (Ref. 5) discovered that the sliding of soil particles occurs in the plane in which the ratio of shear stress to normal stress has its maximum value, which they called the
mobilized plane. They defined the yield surface as
where the parameter μ =
(τ/
σn)STP equals the maximum ratio between shear stress and normal stress in the
spatially mobilized plane (STP-plane), and the invariants are applied over the effective stress tensor (this is the stress tensor minus the fluid pore pressure).
and ϕ denotes the angle of internal friction in the Mohr–Coulomb criterion.
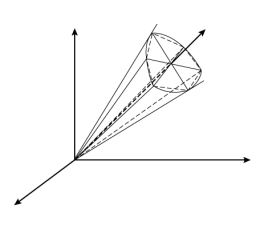
where I1 and
I3 are the first and third stress invariants, respectively, and
k is a parameter related to the direction of the plastic strain increment in the triaxial plane. The parameter
k can vary from 27 for hydrostatic stress conditions (
σ1 =
σ2 =
σ3), up to a critical value
kc at failure. In terms of the invariants
I1,
J2, and
J3, this criterion can be written as
with ϕ as the angle of internal friction in the Mohr–Coulomb criterion.
here, σm is the maximum mean stress and
p = −I1/3 is the pressure, which is negative in tension.
A key concept for porous plasticity models is the evolution of the relative density, which is the solid volume fraction in a porous mixture. The relative density is related to the porosity (or void volume fraction)
ϕ by
Shima and Oyane (Ref. 9) proposed a yield surface for modeling the compaction of porous metallic structures fabricated by sintering. The criterion can be applied for powder compaction at both low and high temperatures. The yield function and associated plastic potential is defined by an ellipsoid in the stress space. The plastic potential
Qp is written in terms of both von Mises equivalent stress and mean pressure, and it also considers isotropic hardening due to changes in porosity. The plastic potential is defined by
here, σe is the equivalent stress,
σys0 is the initial yield stress,
pm is the pressure, and
ρrel is the relative density. The material parameters
α,
γ, and
m are obtained from curve fitting experimental data. Typical material parameter values for copper aggregates are
α =
6.2,
γ =
1.03, and
m =
5.
The Gurson criterion (Ref. 10) consists in a pressure dependent yield function to describe the constitutive response of porous metals, this yield function is derived from the analytical expression of an isolated void immersed in a continuum medium. The void volume fraction, or porosity
ϕ, is chosen as main variable. The yield function and associated plastic potential is not an ellipse in the stress space, as in
The Shima–Oyane Criterion, but it is defined in terms of the hyperbolic cosine function. The plastic potential for the Gurson criterion reads
here, σe is the equivalent stress,
σys0 is the initial yield stress,
pm is the pressure, and
ϕ is the porosity.
Tvergaard and Needleman modified The Gurson Criterion for porous plasticity to include parameters to better fit experimental data (
Ref. 11-
12). The resulting criterion is called the Gurson–Tvergaard–Needleman (GTN) criterion in the literature. The plastic potential for the GTN criterion reads
here, σe is the equivalent stress,
σys0 is the initial yield stress,
pm is the pressure, and
ϕe is the effective void volume fraction (effective porosity). Typical correction parameter values are
q1 =
1.5,
q2 =
1.03, and
q3 =
q12.
The effective void value fraction (or effective porosity) ϕe used in the plastic potential is a function of the current porosity
ϕ and other material parameters. It is often given using a bilinear definition
where ϕc is the critical void volume fraction (critical porosity) at which void coalescence begins, and
ϕf is the void volume fraction at failure. When the porosity increases up to the value of failure, the effective porosity takes a maximum value of
ϕm and the porous material loses the capacity to carry stresses. The maximum porosity value is derived from other parameters
Since typical values for the parameters are q3 =
q12, the maximum porosity value is given by
ϕm = 1/q1.
A similar definition for ϕe that gives a smoother response as the material reaches failure can was suggested in
Ref. 14. It is based on a modification such that the effective void volume fraction reaches its maxim value asymptotically
where ϕi = 0.75(ϕf − ϕc) + ϕc, and
The Fleck–Kuhn–McMeeking criterion (Ref. 15), also called the FKM criterion, was developed to model the plastic yielding of metal aggregates of high porosity. The yield function and associated plastic potential is derived from expressions for randomly distributed particles. The criterion is considered relevant for aggregates with porosity between 10% and 35%. The plastic potential for the FKM criterion reads
here, σe is the equivalent stress and
pm is the pressure. The
flow strength of the material under hydrostatic loading,
pf, is computed from
here, σys0 is the initial yield stress, and
ϕ is the void volume fraction (porosity). The maximum void volume fraction
ϕm typically takes the value of 36%, the limit of dense random packing of sintered powder.
The FKM–GTN criterion is a combination of The Fleck–Kuhn–McMeeking Criterion and
The Gurson–Tvergaard–Needleman Criterion, intended to cover a wider range of porosities (
Ref. 16–
17). The GTN model is used for low void volume fractions (porosity lower than 10%), and for void volume fractions higher than 25%, the FKM criterion is used. In the transition zone, a linear combination of both criteria is used.
Since the relative density is related to the porosity ϕ by
ρrel =
1 − ϕ, the change in porosity is also controlled by the change in plastic volumetric strain
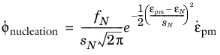 for
for 
here, εN is the mean strain for nucleation,
fN is the void volume fraction for nucleating particles, and
sN is the standard deviation. Typical values for these parameters are
εN =
0.04,
sN =
0.1, and
fN =
0.04. It is assumed that nucleation appears only in tension, and that there is no nucleation in compression.
here, kw is a material parameter,
ϕ is the current porosity,
nD is a deviatoric tensor coaxial to the stress tensor, and
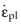
is the plastic strain rate, which depends on the porous plasticity model. The weight
w is computed from stress invariants as
where θ is the
Lode angle. The weight variable has a value of
w =
0 at the compressive and tensile meridians (
θ =
0 and
θ =
π/3), and it attains its maximum
w =
1 for
θ =
π/6.
now depends on the initial yield stress σys0, the hardening function
σh, and the equivalent plastic strain in the porous matrix
εpm.
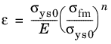 for
for 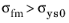
where σys0 is the initial yield stress,
n is the hardening exponent, and the Young’s modulus
E is taken from the elastic material properties. By writing the onset of plasticity as
ε0 =
σys0/E, and noting that
ε =
ε0 +
εpm for
σfm >
σys0, this reads
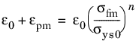 for
for 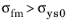
where “old” denotes the previous time step and Λ = λΔt, where
Δt is the pseudo-time step length.
For large plastic strains, Equation 3-55 is numerically solved with the so-called
exponential mapping technique
For each Gauss point, the plastic state variables (εp or
Fp−1, depending on whether small strain or large strain plasticity is selected) and the plastic multiplier,
Λ, are computed by solving either of the above time-discretized flow rules together with the complementarity conditions
|
|
The numerical tolerance to fulfill the condition Fy = 0 is given in SI units of Pascals, and it depends on the initial yield stress (in case of plasticity and porous plasticity) or it is defined in terms of other material parameter (for soil plasticity).
|
|
•
|
Relative tolerance. To check the convergence of the local plasticity equations based on the step size. The final tolerance is computed based on the current solution of the local variable and the entered value. The default value is 1e-6.
|
To display the Advanced section, click the
Show More Options button (

) and select
Advanced Physics Options in the
Show More Options dialog box.
As plasticity is rate independent, the plastic dissipation density Wp is obtained after integrating an extra variable in the plastic flow rule.
|
|
When the Calculate dissipated energy check box is selected, the plastic dissipation density is available under the variable solid.Wp and the total plastic dissipation under the variable solid.Wp_tot.
|
The nonlocal plasticity model implemented in COMSOL Multiphysics is based on the so-called implicit gradient method suggested in Ref. 23, and it incorporates some of the generalizations introduced by the micromorphic theory (
Ref. 24). The theory assumes that the free energy of the elastoplastic material not only depends on the macroscopic displacement
u and macrostate variables, such as the equivalent plastic strain
εpe, but also on some micromotion
ϕ and its gradient. If the micromotion variable is identified as a nonlocal version of the equivalent plastic strain,
εpe,nl, the free energy potential is written as
(3-65)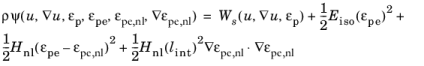
here Ws is the elastic free energy,
Hnl is a model parameter that determines the strength of the coupling between the macro- and micromotions, and
lint is the length scale that determines the influence radius of the interaction. For simplicity,
Equation 3-65 assumes linear isotropic hardening, but the same concept is applicable for more general isotropic hardening laws and can for example also be extended with kinematic hardening.
Taking the variation of Equation 3-65 with respect to state variables
εpe,
εpe,nl, and
∇εpe,nl leads to the following set of equations related to the plasticity model:
here, Ω is the domain of the elastoplastic problem. Variation of
Equation 3-65 with respect to the remaining state variables leads to the standard elasticity equations. In the nonlocal (or regularized) plasticity problem,
εpe,nl is an additional dependent variable that is solved as part of the global problem. The structure of the local plasticity problem is not changed and the numerical solution remains the same as discussed above, but the hardening law now depends on
εpe,nl.
For porous plasticity, the same equation applies, but εpe and
εpe,nl are replaced by the equivalent plastic strains in the matrix material,
εpm and
εpm,nl. It is also possible to add nonlocal effects to the void volume fraction
ϕ.
The porous plasticity model is then extended with the following set of equations
where ϕnl is the nonlocal void volume fraction. In contrast to the equivalent plastic strain, it is assumed that there is a perfect coupling between
ϕ and
ϕnl, and that the nonlocal void volume fraction
ϕnl directly replaces its local counterpart in the model equations.
Add a Set Variables subnode to the
Plasticity,
Porous Plasticity,
Soil Plasticity, or
Elastoplastic Soil Models to set up the plastic strain tensor, plastic deformation gradient, the equivalent plastic strain, and other internal elastoplastic variables.
