You are viewing the documentation for an older COMSOL version. The latest version is
available here.
where K is the bulk modulus and
G is the shear modulus. By using the convention that the pressure is the mean stress defined as positive in compression,
For a body subject to pure torsion on the plane 12, the stress tensor components are zero except the shear stress σ12 = σ21 = τ, and also the elastic strain tensor has zero components beside the shear strains on that plane
ε12 = ε21 = γel/2.
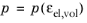 and
and 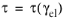
The tangent shear modulus Gt(γel) and the secant shear modulus
Gs(γel) in the most general case depend nonlinearly on the shear strain, and are defined as
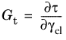 and
and 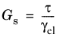
Note that the secant modulus is sometimes called the chord modulus between zero and current strain level.
The tangent bulk modulus Kt(εel,vol) and the secant bulk modulus
Ks(εel,vol) depend on the elastic volumetric strain, and are defined as
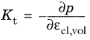 and
and 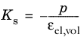
For linear elastic materials, it is clear that Gt = Gs = G and
Kt = Ks = K, but this is not the case for nonlinear elastic materials.
The Ramberg–Osgood material model (Ref. 1) is a nonlinear elastic material commonly used to model plastic deformation in metals, but it also often used in soil engineering. As it is an elastic model, it can only represent plasticity during pure on-loading conditions.
Here, E means the initial Young’s modulus, and
εref is the strain at a reference stress
σref. The parameter
n is the stress exponent. It is common to use
εref = 0.002, so
σref is the stress at
0.2% strain, typically denoted by the symbol
σ0.2. This parameter has several names depending on the literature:
0.2% offset yield strength,
0.2% proof stress,
0.2% proof strength, or
0.2% yield stress. Typical values for stainless steel are
E = 200 GPa,
σ0.2 = 600 MPa, and
n = 4.8.
In order to avoid a circular dependence of internal variables, the nonlinear strain εnl is defined with an auxiliary degree of freedom, so the stress reads
σ = E(ε − εnl).
(3-28)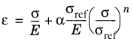
so at the reference stress σref, the strain is
ε = (1 + α)σref/
E. It is common to use
α = 3/7, so
σref represents the stress level at which the secant Young’s modulus has been reduced to 70% its initial value:
E0.7 = E/(1 + α) = 0.7E. At this reference stress the strain is
ε = σref/
E0.7.
|
•
|
For n > 1 the material behaves as a dilatant (shear-thickening) solid
|
|
•
|
For n = 1 the material is linear elastic
|
|
•
|
For 0 < n < 1 the material behaves as pseudoplastic (shear-thinning) solid
|
|
•
|
For n = 0 the material is perfectly plastic
|
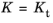 for εel,vol > 0
for εel,vol > 0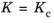 for εel,vol < 0
for εel,vol < 0where εel,vol is the volumetric strain,
Kc is the bulk modulus for compression, and
Kt the bulk modulus for tension.
If only the uniaxial behavior is measured, the measurements do not fully define the material behavior. An extra assumption is needed. The Uniaxial data material model allows you to assume either a constant Poisson’s ratio, or a constant bulk modulus. Also, if only uniaxial extension data is available, further assumptions are needed for covering the uniaxial compressive behavior of the material.
For the uniaxial tensile test, the axial stress corresponds to the principal stresses σax = σ1 = σmises, and the other two principal stresses are equal to zero,
σ2 = σ3 = 0.
The principal (axial) strain is positive in tension, εax = ε1, and the other two (transverse) strains are negative and related by the Poisson’s ratio
ε2 = ε3 = −νε1.
For uniaxial compression, the axial strain is negative, and when the principal strains are sorted as ε1 > ε2 > ε3 it corresponds to the third principal strain,
εax = ε3. The other two (transverse) strains are positive and related by the Poisson’s ratio
ε1 = ε2 = −νε3. Also, the axial stress is negative in compression, and it corresponds to the third principal stress
σax = σ3 = −σmises. The other two transverse stresses are zero
σ1 = σ2 = 0.
Here, Es is the secant Young’s modulus, and the axial stress
σax is considered as a function of the elastic axial strain
εax. Thus
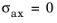 when
when 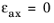
|
|
The elastic axial strain εax can be called in user defined uniaxial stress functions by referencing the variables solid.eax, where solid is the name of the physics interface node. See also the description of the Uniaxial Data material model in the Solid Mechanics interface documentation.
|
Here, the secant shear modulus Gs is constant for Linear Elastic materials, but in general one could use a nonlinear relation. It is possible to use shear data to define the shear stress as a function of elastic shear strain as follows:
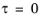 when
when 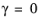
With the help of the secant shear modulus Gs computed from shear data, Hooke’s law simplifies to
where K is the bulk modulus.
|
|
The elastic shear strain γ can be called in user defined shear stress functions by referencing the variables solid.esh, where solid is the name of the physics interface node. See also the description of the Shear Data material model in the Solid Mechanics interface documentation.
|
where the strain exponent n and a reference shear strain
γref control the shape of the hyperbola.
For hyperbolic material models, the maximum shear modulus occurs at zero shear strain, so practitioners might call G the “maximum shear modulus” and use the notation
Gmax. Sometimes it is also called “small strain shear modulus”.
The Hardin–Drnevich model (Ref. 3) is a hyperbolic soil model (with
n = 1) defined by two input parameters: the initial shear modulus
G and a reference shear strain
γref:
Since τ = Gsγ, the shear stress is bounded by
τmax = Gγref as the shear strain increases.
The hyperbolic Hardin–Drnevich model is normally used for quantifying stiffness reduction curves in soils. Commonly, the reference shear strain γref is replaced by the reference shear strain at which the secant shear modulus has been decreased to 70% of its initial value. Calling this shear strain value
γ0.7, the reference strain is written as
so that when γ = γ0.7 the secant shear modulus is
Gs = 0.7G.
The original model was originated by Kondner to fit triaxial test data for undrained soils. Duncan and Chang (Ref. 4) and other coworkers (
Ref. 5) developed this hyperbolic model to its current state. The material model is written in terms of the axial and radial stresses
σ1 and
σ3 and the axial strain
ε, and it describes the stress-strain curve by fitting the hyperbola
here a and
b are material parameters obtained by curve fitting data from the triaxial test. The parameter
a is related to the initial Young’s modulus
E
and the parameter b defines the asymptote of the hyperbola, which is related to the ultimate value of
σ1 − σ3 denoted
qult
The ultimate value qult is related to the strength of the soil.
For the triaxial test, the axial strain ε is related to the shear strain
γ by the Poisson’s ratio as
Since the initial shear modulus is related to the initial Young’s modulus as G = E/2(1 + ν), this stress-strain relation can alternatively be written as
The Duncan–Selig model is a combination of the Duncan’s hyperbolic material model (Ref. 4,
Ref. 5) and Selig’s model to describe nonlinear bulk modulus behavior. Selig (
Ref. 6) further developed the model of Duncan and others in order to include a nonlinear volumetric response in soils.
where εel,vol is the volumetric strain, and
εult is the asymptote of the hyperbola, the maximum value for the volumetric compression. Note that
K represents the bulk modulus at zero strain.
The small strain overlay model (Ref. 26,
Ref. 27) incorporates both the nonlinear stiffness and hysteresis effects by utilizing a nonlinear shear modulus derived from the shear strain history observed over multiple loading–unloading cycles.
where εel,dev and
εel,vol are the deviatoric and volumetric elastic strains, and
εr,dev,
εr,vol, and
σr are the deviatoric and volumetric elastic strains and stress at the last load reversal point.
The secant shear modulus is defined from an Hyperbolic Law, in a similar way as done for the
Hardin–Drnevich model. The
secant shear modulus for primary loading is defined by two input parameters, the initial shear modulus
G0 and a reference shear strain
γref, as
Here, γhist is a measure of the shear strain history. In
Ref. 26, the reference shear strain is defined from
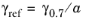
, where
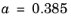
is a tuning parameter that fits experimental data and
γ0.7 is the shear strain at which the secant shear modulus has been decreased to 70% of its initial value.
The secant shear modulus for unloading and reloading is defined as
The load path is considered as primary loading if the soil has not reached any load reversal stage, in which case
Gpl is used. When a load reversal happens, the soil is assumed to be on the unloading–reloading path, and
Gur, is instead used.
|
|
The elastic volumetric strain εvol,el can be called in user defined expressions by referencing the variables solid.eelvol, where solid is the name of the physics interface node.
|