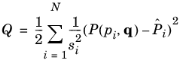Parameter Estimation
Hyperelastic components like seals, insulators, soft sensors, and actuators frequently exhibit a nonlinear stress-strain response. Viscoelastic models for rubber and soft biological tissues display strain-rate sensitivity and hysteresis during cyclic loading. Likewise, metals and alloys demonstrate ratcheting and nonlinear responses under cyclic loading. To ensure precise predictions of these components’ behavior, it is imperative to calibrate nonlinear material models using an extensive dataset of experimental results.
With the Nonlinear Structural Materials Module, you can calibrate the model parameters of any built-in and user-defined material model to experimental data using nonlinear least-squares Parameter Estimation techniques. The Parameter Estimation functionality is available in COMSOL Multiphysics in the context menu of a Component or under Optimization in the Physics toolbar. Each Global Least-Squares Objective subnode adds an objective function Q to the model, which is of the form
(2-42)
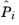
Herein, pi represents an experimental parameter (for example, applied stretch or time), is the corresponding experimental value (for example, measured stress), and P(pi, q) is the corresponding model prediction. The quantity si is a scale that weighs the terms in the objective function and ensures that Q is dimensionless.
The model expression P normally depends implicitly on the model parameters q through the solution of the forward problem. To solve the inverse problem, the forward model and the objectives need to be combined with a study containing a Parameter Estimation study step. When multiple objectives are selected in the study step, the total objective function that is minimized is the sum of all the objective functions selected. During the parameter estimation study, the forward problem will be solved multiple times for different values of the model parameters, so it is good practice to first set up and test the forward model before running a parameter estimation study.
Three optimization solvers are available with the Nonlinear Structural Materials Module in the Parameter Estimation study step: the derivative-free BOBYQA solver, and the gradient-based IPOPT and Levenberg–Marquardt solvers. To avoid finding unphysical regions in the parameter space, it is possible to specify bounds on the parameters. For most least-squares problems, the default Levenberg–Marquardt algorithm with a finite difference approximation of the Jacobian is a robust and efficient choice of optimization solver.
By default, the Levenberg–Marquardt solver is set to terminate if either the increment of the (scaled) parameters or the maximum angle between the error vector and the Jacobian is smaller than a given optimality tolerance (default to 1e-3). In the settings of the Optimization Solver, it is possible to include an additional termination criterion based on the relative change of the objective function by selecting the Terminate also for defect reduction check box, which can be useful if the solver reaches a relatively flat local minimum in the parameter space. The default termination criteria are normally more robust, however.
To monitor the progress of the optimization visually, is it possible to set up a plot while solving that compares the current model prediction with the experimental data.
For further information about the Parameter Estimation functionality and the optimization solvers, see
•
Parameter Estimation and Global Least-Squares Objective in the Optimization Module User’s Guide.
•
The Parameter Estimation Study in the Optimization Module User’s Guide.
•
The Levenberg–Marquardt Solver in the Optimization Module User’s Guide.
For examples showing how to set up a parameter estimation study, see
•
Parameter Estimation of Hyperelastic Materials: Application Library path Nonlinear_Structural_Materials_Module/Hyperelasticity/parameter_estimation_hyperelasticity.
•
Parameter Estimation of Elastoplastic Materials: Application Library path Nonlinear_Structural_Materials_Module/Plasticity/parameter_estimation_plasticity.
•
Parameter Estimation of Viscoplastic Polymers: Application Library path Nonlinear_Structural_Materials_Module/Viscoplasticity/parameter_estimation_polymer_viscoplasticity.