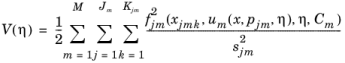where M is the number of series (measurement series), Jm is the number of measurements, and Kjm is the number of points. The variable x is the space coordinates, η are the parameters for which the cost function should be minimized and um(x, p, η) solves a given PDE or ODE. The variable p is time if the PDE or ODE is time dependent, but it can also represent any parameter when the forward problem is stationary. Each measurement series can be associated with a set of parameters, Cm. 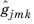The functions sjm are the scales, and fjm represent the difference between some model function gjm and some measured data ; that is, fjm can be written as

The Levenberg–Marquardt algorithm as implemented in the Optimization Module relies on two fundamental ideas: evaluation of an approximate Hessian and regularization of the Hessian approximation. The special structure of least-squares objective functions allows cheap evaluation of an approximate Hessian (matrix of second derivatives), which can in principle be used directly in a Newton iteration. However, least-squares problems are also often ill-conditioned, making the full Newton process unstable. Therefore, the Hessian is modified using a regularization parameter to guarantee its positive definiteness. This parameter is updated between iterations, based on the success or failure of the previous step. For further details, see Ref. 10.