Common Study Step Settings
The study step nodes’ Settings windows contain the following sections (in addition to specific study settings for each type of study step):
The Study Steps Settings Windows’ Toolbar
On top of the study steps Settings windows, a toolbar contains the following commands:
•
Click Compute () or press F8 to compute the entire study. If there is an enabled Solver node under Solver Configurations, that solver sequence will be executed. Otherwise a new solver sequence will first be generated. See Computing a Solution.
•
Click Update Solution () or press F5 (when applicable) to update the current study. See Updating a Solution.
Study Settings
Include Geometric Nonlinearity Check Box
If you have a license for the Acoustics Module, MEMS Module, or Structural Mechanics Module (including any add-on modules such as the Nonlinear Structural Materials Module) and your model involves structural mechanics, then the Study Settings section includes an Include geometric nonlinearity check box.
Select the Include geometric nonlinearity check box to enable a geometrically nonlinear analysis for the study step. Some physics designs force a geometrically nonlinear analysis, in which case it is not possible to clear the Include geometric nonlinearity check box. For further details, see the theory sections for the respective physics interface in the applicable modules’ manuals.
Results While Solving
This section is empty and unavailable when results while solving is not used or not applicable; for example, it is empty when there is an outer Parametric Sweep or Optimization active (and when no Auxiliary Sweep or Load Cases are used) and when you have enabled adaptive mesh refinement in the Stationary study step.
Select the Plot check box to allow plotting of results while solving. Then select what to plot from the Plot group list. The Default options creates the first default plot if it does not exist; otherwise, it uses the first default plot or the latest plot that you have added. The software plots the dataset of the selected plot group as soon as the results become available. Select Times stored in output (the default) or Time steps taken by solver from the Update at list when applicable.
Use the Probes list to select any probes to evaluate. The default is All, which selects all probes for plotting and tabulation of probe data. Select Manual to open a list with all available probes. Use the Move Up (), Move Down (), Delete (), and Add () buttons to make the list contain the probes that you want to see results from while solving. Select None to not evaluate any probe.
The software plots the dataset of the selected plot group and probes as soon as the results become available. Select Steps stored in output (the default) or Steps taken by solver from the Update at list.
You can use probes to tabulate values of interest during a large parametric simulation, for example. It can then be possible to keep only the last solution in memory during the parametric sweep, which potentially can significantly reduce memory requirements and the simulation time.
Physics and Variables Selection
See Physics and Variables Selection for detailed information about this section. You can control and specify different cases where the physics interface to solve for is varied, or, for various analysis cases, which variables and physics features (for example, boundary conditions and sources) to use. The default is to solve for all physics interfaces that are compatible with the study step type.
Values of Dependent Variables
When you have physics interfaces in a study step that you do not solve for but that provide degrees of freedom, you can specify how the COMSOL Multiphysics software handles the values of such degrees of freedom (dependent variables).
The settings in this section determine how the solver handles dependent variables that you do not solve for. This is applicable in, for example, a solver configuration where you only solve for a subset of the dependent variables in each step. You can also specify the initial values of variables that you do solve for.
By default, the COMSOL Multiphysics software determines these values heuristically depending on the physics as, for example, the specified initial values or a solution from an earlier study step. Under Initial values of variables solved for, the default value of the Settings list is Physics controlled. To specify the initial values of the dependent variables that you solve for, select User controlled from the Settings list.
The Initial values of variables solved for settings have no effect when using the eigenvalue solver.
Similarly, to specify the values of dependent variables that you do not solve for, select User controlled from the Settings list under Values of variables not solved for.
Then use the Method list to specify how to compute the initial values of variables solved for and the values of variables not solved for. Select:
•
Initial expression to use the expressions specified on the Initial Values nodes for the physics interface in the model.
•
Solution to use initial values as specified by a solution object (a solution from a study step).
Use the Study list to specify what study to use:
•
Select Zero solution to initialize all variables to zero.
•
Select any other available study to use it as an initial value.
Then use the Solution list to specify what solution object to use if Study has been set to a study:
-
Current to use the current solution.
-
Any other available solution object to use it as initial value.
Depending on the solution object to use, you can choose different solutions to use. If a solution has nodes for storing solutions in its sequence, you can choose which solution to use using the Use list. The Current value is the value that the solution has at the moment the value is read. The other values are the values stored in the respective nodes of the sequence. Choose Manual to enter the index for the solution that you want to use. The index can be a global parameter that is swept in a Parametric sweep with solution number inputs to it.
Depending on the study type of the solution that you selected, you can choose different solutions from a list underneath the Study list (and the Solution and Use lists, if present):
For a Stationary study, from the Selection list, select one of the following options:
•
Automatic (single solution) (the default) to select one solution on the Dependent Variables node depending on a global evaluation to find the current value of the parameters in the input solution or, if that is not possible, the last (typically the only) solution.
•
Automatic (all solutions) to use all (typically just one) solutions from that study (see below for more details).
•
First to use the first (typically the only) solution
•
Last to use the last (typically the only) solution, select From list to pick solutions from a list.
•
Interpolated to specify an interpolated value in the text field below.
•
Manual to use a specific solution number that you specify in the Index field.
•
1 to use the first (typically the only) solution. If you use a parametric continuation of the stationary study, there can be additional solutions to choose from.
For a Time Dependent study, from the Time list, select one of the following options:
•
Automatic (single solution) (the default) to select one solution on the Dependent Variables node depending on a global evaluation to find the current value of the parameters in the input solution or, if that is not possible, the solution for the last time.
•
Automatic (all solutions) to use all solutions from that study (see below for more details).
•
First to use the first solution.
•
Last to use the last solution.
•
Interpolated to specify a time in the text field below.
•
Manual to use a specific solution number that you specify in the Index field.
•
One of the output times to use the solution at that time.
For an Eigenvalue or Eigenfrequency study, from the Eigenvalues list, select one of the following options:
•
Automatic (single solution) (the default) to select one solution on the Dependent Variables node depending on a global evaluation to find the current value of the parameters in the input solution or, if that is not possible, to use the solution for the first eigenvalue or eigenfrequency and its associated eigensolution.
•
Automatic (all solutions) to use all solutions from that study (see below for more details).
•
First to use the first solution.
•
Last to use the last solution.
•
Interpolated to specify an eigenvalue of eigenfrequency in the text field below.
•
Manual to use a specific solution number that you specify in the Index field.
•
One of the eigenvalues to use the solution for the corresponding eigensolution.
For a parametric or Frequency Domain study, from the Parameter value list, select one of the following options:
•
Automatic (single solution) (the default) to select one solution on the Dependent Variables node depending on a global evaluation to find the current value of the parameters in the input solution or, if that is not possible, the solution for the last parameter value set or frequency.
•
Automatic (all solutions) to use all solutions from that study (see below for more details).
•
First to use the first solution.
•
Last to use the last solution.
•
Interpolated to specify a time in the text field below.
•
Manual to use a specific solution number that you specify in the Index field.
•
One of the parameter value sets or frequencies to use the corresponding solution.
For the Automatic (all selections) option, all solutions are passed down to the solver, and the solver selects the initial values based on if there is a match to the current parameter tuple. This makes it possible to pass multiple initial values or guesses to the solver, which can be useful if you are doing a parametric study using multiple parameters and the convergence of each parameter tuple is dependent on a good initial guess. It can also be used together with the time-dependent parametric solver to use different initial values for each parameter tuple.
Store in Output
In the Store in Output section, you can specify to store the field variables that you solve only for some parts of the geometry (a boundary, for example, if the solution in the domain is not of interest). You define the parts of the geometry for which to store the fields as selection nodes.
For each listed physics interface, choose one of the following options in the Output column:
•
Choose Physics controlled (the default) to use the physics interface control what to store in the output.
•
Choose All to store all fields in all parts of the geometry where they are defined.
•
Choose None to not store any field in the output.
•
Choose Selection to choose one or more selections that you add to the corresponding row in the Selection column. Then, under Selections, click the Add button () to open an Add dialog box that contains all of the available selections. Select the selections that you want to add and then click OK. You can also delete selections from the list using the Delete button () and move them using the Move Up () and Move Down () buttons.
See also the Field node, where you can also control what to store in the output, if the corresponding Dependent Variables uses user-defined settings.
If you use For selection and store the solution only for some parts of the geometry, it is not possible to continue with another study step.
Mesh Selection
Specify — for each geometry — which mesh to use for the study step. For each geometry listed in the Component column, select a mesh from the list of meshes in the Mesh column. Each list of meshes contains the meshes defined for the geometry that you find on the same row.
Adaptation and Error Estimates
These are settings for mesh adaptation and error estimates, available for stationary, eigenfrequency, eigenvalue, and frequency-domain study steps. Mesh adaptation (with other settings and operation) is also available for time-dependent study steps; see Time Dependent and Adaptive Mesh Refinement (Time-Dependent Adaptation). Depending on the type of adaptation, meshing sequences for the adaptive mesh refinements, using Adapt or Size Expression nodes, and corresponding solutions are created for inspection and possible modification. Error estimates are available as variables for postprocessing (for example, freq.errtot for the total error estimate in a Frequency Domain study). The adaptive mesh refinement solutions become available in a separate Solution dataset (Study 1/Adaptive Mesh Refinement Solutions 1, for example). When using that dataset for postprocessing, you can choose to use any of the available adaptive mesh refinement solutions from a Parameter selection (Refinement level) list. Additional settings are available in the Adaptive Mesh Refinement (Stationary and Eigenvalue Adaptation) and Error Estimation subnodes under the solver node in the solver configurations.
From the Adaptation and error estimates list, select Error estimates if you want to use error estimation or select Adaptation and error estimates if you want to use adaptive mesh refinement. In the latter case, error estimates that are used in the adaptation algorithm are also available for postprocessing. Choose None for no adaptation or error estimation. The internal name for the refinement level parameter is adaptlevel. It is added by the adaptation solver method to separate the solutions for the different meshes. In the case that there is a user-defined parameter with that name in the model, a unique name for the refinement level parameter is made by adding a digit to adaptlevel. You can use it to access the solutions from different mesh refinement levels using the withsol() operator with; for example, using the following syntax: withsol('sol1',expr,setval(adaptlevel,2)) to evaluate an expression expr with the solution in sol1 for the mesh adaptation level 2.
•
The Adaptive Solver Algorithms and Error Estimation
•
Error Estimation — Theory and Variables
•
Adapt — the Adapt node in a meshing sequence also provides mesh adaptation. It includes a selection of geometric entities, which can be useful if you want to limit the mesh adaptation to certain geometric entities (some but not all domains, for example).
The software performs adaptive mesh refinement in one geometry only. Use the Adaptation in geometry list to specify that geometry. If you do not want to perform the mesh adaptation in the entire geometry, use the settings in the Geometric Entity Selection for Adaptation section below.
Use the Error estimate list to control how the error estimate is computed:
•
Select L2 norm of error squared to use the squared L2 norm of the error. This is the only option for Eigenvalue studies. In the Error Estimation node under the Stationary Solver node, use the Scaling factor field to enter a space-separated list of scaling factors, one for each field variable (default: 1). The error estimate for each field variable is divided by this factor. Also, the L2 norm error estimate is based on a stability estimate for the PDE. Also in the Error Estimation node, use the Stability estimate derivative order field to specify its order (default: 2). For certain problems, which are symmetric and where strong error estimates hold, this method is equivalent to a functional error estimation with the functional being the L2 norm squared of the solution. This method can be used also for problems where these assumptions do not hold, but then the adaptation will not be optimal. See the following for some more in-depth information about these settings.
The L2 norm of error squared method estimates the error for a mesh element as a summation of contributions for the different equations solved for. It sums over
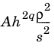
where A is the element area (volume, length), h is the element size, q is the Stability estimate derivative order, s is the Scaling factor, and ρ is an estimate of the PDE residual. The asymptotic behavior for ρ is that it is proportional to hp, where p is the Residual order (see below). Even if it is possible to estimate the actual value for ρ very generally, assisting the algorithm with this order is important — for example, for the Element selection method Rough global minimum (in the Adaptive Mesh Refinement subnode; see Adaptive Mesh Refinement (Stationary and Eigenvalue Adaptation)), which essentially solves an optimization problem for where to refine so that the total error is reduced as much as possible (constrained by how many elements that can be added). All of the values for the Stability estimate derivative order, Scaling factor, and Residual order (q, s, and p, respectively, in the Error Estimation subnode; see Error Estimation) can all be given as vectors for the different equations. For the Stability estimate derivative order, the default is 2, and it is related to the stability estimate that holds for the problem at hand. If it is not of a Poisson type, then it might need adjustment. For the Scaling factor, the default is 1. It is mainly important to relatively weigh in the different parts of the equations solved for, which means that you need to give a space-separated array of numbers in general. Notice that when solving a multiphysics problem, the summation over different equations will not have the same unit since the different ρ will have different units. So, a first effort with scaling would be to take this into account. In fact, not even a single-physics case like fluid flow will make this summation unit consistent because the residual for momentum and mass conservation will be added up with the default scaling factors of 1. For the Residual order, the default is one order lower than the shape functions used for the equation. Change this only for nonstandard PDEs. Roughly speaking, the expected order is the basis order minus the highest spatial derivative order in the weak formulation. For a second-order PDE formulation with an integration by parts (lowering all second-order derivatives to first order) this will be of order one.
•
Select Functional and specify a Functional type. Available functional types are Predefined and Manual. This option adapts the mesh toward improved accuracy in the expression for the functional (for example, some energy, drag, or lift). Select Manual to specify a globally available scalar-valued expression in the Functional field (for example, the name of a global variable probe). If you select Predefined, you can choose from a predefined list of functional from the Solution functional list:
-
 Integral (the default)
-
 L2 norm
-
 L1 norm
-
 Approximate max norm
For a Stationary study step stat, a global variable is defined for the functional with the name stat.gfunc (and similarly for a frequency-domain study step). The functional can be evaluated under Results>Derived Values by adding a Global Evaluation node and, in the Expressions section in its Settings window, selecting Global Definitions>
Error estimation>stat.gfunc - Functional - Stationary.
The functional must be differentiable (or complex-valued analytic). Also, the expressions in the formulation must be differentiable. If this does not hold, the adjoint solution and its error estimate risk not being accurate, and the adaptation will then not be optimal for the functional used. The Functional option estimates the error for a mesh element as a summation of contributions. It sums over A ωK ρ, where ωK is computed from the adjoint (or dual) solution. ωK can be computed with different methods (PPR for Lagrange or Interpolation error). Equation 20-5 is about how ωK is computed for PPR for Lagrange. Notice that this method is not using scaling factors or the stability estimate derivative order because they are not part of the formula (they are built into ωK). But ρ is part of the formula and the residual order can therefore be important (for example, for the Rough global minimum method; see Adaptive Mesh Refinement (Stationary and Eigenvalue Adaptation)). For the Approximate max norm, high order p-norm. The reason for this is that it is possible to differentiate this functional.
•
Select Error indicator to specify an error indicator using an error expression, which you add to the Error expression table below using the Add () button. The error expression can be any expression, including field variables and their derivatives, defined in the domain. This method will adapt the mesh where the error expression becomes large; the adaptation is typically not optimal. Select the Active check box for the error expressions that should be part of the error indicator. Use the Move Up (), Move Down (), and Delete () buttons as needed to rearrange and remove error expressions. With this setting, there are no additional settings in the Error Estimation subnode, which becomes unavailable.
From the Add Error estimation variables list (not available if you chose Error indicator from the Error estimate list above), choose which variables to store, if any:
•
Select Error estimates and residuals to store all variables (the default).
•
Select Error estimates to store only the variables for error estimation.
•
Select None to not store any variables, which may lead to performance improvements.
The Save solution on every adapted mesh check box is selected per default. Clear this check box if you do not want to save solution on every adapted mesh. In that case, the last two solutions are saved (the finest one and the second finest) regardless of the total number of solutions.
Under Mesh adaptation, the following settings are available.
Use the Adaptation method list to control how to adaptively refine mesh elements. Select one of these methods:
•
 General modification, to use the current mesh as a starting point and modify it by refinements, coarsening, topology modification, and point smoothing. Use the Allow coarsening check box to control if mesh coarsening is used. If the mesh contains anisotropic elements (for example, a boundary layer mesh), it is best to disable mesh coarsening to preserve the anisotropic structure. If you have selected to allow coarsening, specify the Maximum coarsening factor (a value of 5 by default) to scale the refined mesh size in the regions where refinement is not needed.
•
 Rebuild mesh, to set up a size expression describing the error and rebuild the meshing sequence using the size expression as input. Note that structured meshes, such as mapped and swept meshes, in general are not appropriately refined. This method is not supported on imported meshes. The size of the refined mesh is the minimum of the size of the original mesh (previous refined mesh) and the size defined by the refinement. Specify the Maximum coarsening factor (a value of 3 by default) to scale the refined mesh size in the regions where refinement is not needed.
•
 Regular refinement, to make the solver refine elements in a regular pattern by bisecting all edges of an element that needs refinement.
•
 Longest edge refinement, to make the solver refine only the longest edge of an element by recursively bisecting the longest edge of edge elements that need refinement. This method is less suitable for models with nonsimplex elements. This is the default method.
With the settings in the Goal-oriented termination list you or the physics interfaces can add a number of global goal-oriented quantities so that the mesh adaptation will terminate when these are stable to a requested accuracy instead of after a fixed number of adaptation iterations. Choose Off (the default), Auto, or Manual to control. You, when the list is set to Manual, or the physics, when the list is set to Auto, can add a number of global goal-oriented quantities, and the mesh adaptation will terminate when these are stable to a requested accuracy. These goal-oriented quantities could, for example, for an RF simulation be the S-parameters or another quantity of interest. The goal-oriented termination can be used with any of the available error estimation methods. When the Goal-oriented termination list is set to Manual, you can add goal-oriented terminal expressions in the table at the bottom of this section. Click the Add button () to add an expression (default: 1) that you can edit in the Goal-oriented termination expression column. If desired, adjust the tolerance (default: 0.01) in the Tolerance column, and the type of tolerance in the Tolerance type column: Relative (the default) or Absolute. Use the Active buttons to manage which goal-oriented termination expressions to include. The mesh adaptation will run until the relative changes for all expressions (applied individually for all expressions) go below their respective thresholds, unless the maximum number of adaptations limit is met, in which case the algorithm terminates with a warning.
Use the Maximum number of adaptations field to specify the maximum number of adaptive mesh refinement iterations. The default value is 5 in 1D, 2 in 2D, and 1 in 3D. With the Goal-oriented termination set to Auto, the default value is set to 20 in 1D, 15 in 2D, and 10 in 3D.
With the Goal-oriented termination set to Auto or Manual, you can control the display of convergence from the adaptation when the Output goal-oriented termination increments check box is selected. It is possible to choose the plot window to display the convergence as well as the table to be used by the plot from the Plot window — select New window (the default) or Graphics — and Output table lists, respectively. If you choose New from the Output table list, two new tables are created, one for the adaptation convergence plot and one for providing verbose information.
Also choose the level of detail for the log from the Goal-oriented termination log list: Minimal, Normal (the default), or Detailed. Choose Detailed if you want to include the evaluations for all the parameters, frequencies, or eigenvalues in the log.
For additional settings, see Adaptive Mesh Refinement (Stationary and Eigenvalue Adaptation).
Variables for Adaptation and Error Estimation
The following table includes variables that are available when adaptation and error estimates have been enabled. The variable names are for a case with a Stationary study step stat solving for a dependent variable u.
Table 20-4: Variables for Adaptation and Error Estimates.
Variable Name
Description
stat.errEst
The total error summed over all equations and elements. A global variable.
stat.errEst.u
The total error summed over all elements for the equation or variable u. A global variable.
comp1.err.u
The error estimate for equation or variable u in component comp1. It is constant within each mesh element.
stat.errtot
The total error contribution from each element. The summation of errors is over all equations solved for. It is constant within each mesh element.
Geometric Entity Selection for Adaptation
From the Geometric entity level list, choose the geometric entity on which you want to do adaptive mesh refinement: Entire geometry (the default), Domain, Boundary, or Edge (3D only). For example, selecting Boundary can be useful if the model includes a physics interface defined on boundaries (surfaces) and you want to base the adaptation on that physics interface. For all levels except Entire geometry, select the geometric entities to include using the Selection list and selection tools below.
Study Extensions
These are extensions to the study’s main solver, such as adaptive mesh refinement and automatic remeshing. The options vary depending on the study type.
Auxiliary Sweep
Select the Auxiliary sweep check box to enable an auxiliary parameter sweep, which corresponds to a Parametric solver attribute node. For each set of parameter values, the chosen Sweep type is solved for. This functionality is available for Stationary, Time Dependent, and Frequency Domain studies.
Select a Sweep type to specify the type of sweep to perform:
•
Specified combinations (the default) solves for a number of given combinations of values as given for each parameter in the list. The parameter lists are combined in the order given; that is, the first combination contains the first value in each list, the second combination contains all second values, and so on.
•
All combinations solves for all combinations of values; that is, all values for each parameter are combined with all values for the other parameters. Using all combinations can lead to a very large number of solutions (equal to the product of the lengths of the parameter lists).
In the table, specify the Parameter name, Parameter value list, and (optional) Parameter unit for the parametric solver. Click the Add button () to add a row to the table. When you click in the Parameter value list column to define the parameter values, click the Range button () to define a range of parameter values. The parameter unit overrides the unit of the global parameter. If no parameter unit is given, parameter values without explicit dimensions are considered dimensionless.
If you choose Specified combinations, the lists of parameter values must have equal lengths.
An alternative to specifying parameter names and values directly in the table is to specify them in a text file. Use the Load from File button () to browse to such a text file. You can also click the downward arrow beside the Load from File button and choose Load From () to open the fullscreen Select File window. The read names and values are appended to the current table. The format of the text file must be such that the parameter names appear in the first column and the values for each parameter appear row-wise with a space separating the name and values and a space separating the values.
Click the Save to File button () to save the contents of the table to a text file (or to a Microsoft Excel Workbook spreadsheet if the license includes LiveLink™ for Excel®).
Loading and saving the parameter table data using Excel include the units in the Parameter unit column. The unit column is ignored when saving and loading parameter data to *.txt, *.csv, and *.dat files.
For a Stationary or Frequency Domain study, select an option from the Run continuation for list: No parameter or one of the parameters given in the list.
•
Physics and Variables Selection
•
Individual study and study steps are listed in Table 20-2 and Table 20-3.
Continuation is only performed on one parameter, and the other parameters must be kept constant. If one of the secondary parameters varies, then it is considered as a new start for the continuation parameter.
Reuse Solution from Previous Step List
This option is useful for parameters not handled with continuation. Select an option from the Reuse solution from previous step list.
•
No (the default for most studies) to reset the solution to the initial values before each step or continuation sweep. The initial values will not be recalculated by the parametric solver for subsequent parameter values. Parameter dependence of the initial values can be accomplished by using parametric sweep. Set the Reuse solution from previous step to Yes to have continuation if the secondary parameters are also varying.
•
Yes to always use the converged solution from the previous step, or the last solution from the previous continuation sweep (that is, never reset the solution).
•
Automatic (the default for Mean Energies and Reduced Electric Field studies) to normally use the converged solution from the previous step or sweep. However, when multiple parameters are used, the solution from the first step of each parameter list is always used for the first step of the next list.
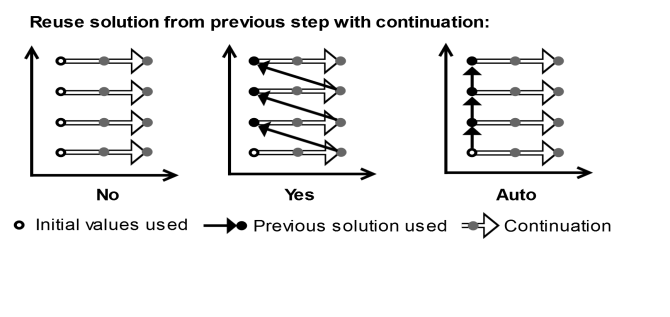
The difference between the three options is shown in Figure 20-2 for a 3-by-4 two-parameter sweep using the different choices for Reuse solution from previous step without continuation:
Figure 20-2: The difference between the three options for a two-parameter sweep without continuation.
When continuation is enabled by setting Run continuation for to one of the parameters, the converged solutions are always reused for the steps along the continuation sweep in this parameter. The setting for Reuse solution from previous step then determines how the solutions are reused between multiple continuation sweeps, if there are additional parameters to sweep over, as shown in Figure 20-3.
Figure 20-3: The difference between the three options for a two-parameter sweep with continuation.
For the Frequency Domain study, the auxiliary sweep is merged with the frequency sweep into a multiparameter sweep with the frequency as the parameter at the innermost level.
See About the Parametric Solver for more information.