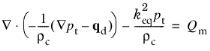The Pressure Acoustics, Frequency Domain Interface exists for several types of studies. Here the equations are presented for the frequency domain, eigenfrequency, and mode analysis studies. All the interfaces solve for the acoustic pressure  p. It is available in all space dimensions — for 3D, 2D, and 1D Cartesian geometries as well as for 2D and 1D axisymmetric geometries.

This is Equation 2-14 repeated with the introduction of the wave number keq used in the equations. It contains both the ordinary wave number k as well as out-of-plane and azimuthal (or circumferential) contributions, when applicable. Note also that the pressure is here the total pressure pt which is the sum of a possible Background Pressure Field pb and the scattered field ps. This enables for a so-called scattered field formulation of the equations. If no background field is present pt = ps = p.

In this equation, p = p(x,ω) = p(x)eiωt (the dependence on ω is henceforth not explicitly indicated). Compute the frequency response by doing a parametric sweep over a frequency range using harmonic loads and sources.

When there is damping, ρc and cc are complex-valued quantities. The available damping models and how to apply them is described in the sections Pressure Acoustics and Theory for the Equivalent Fluid Models.

Equation 2-16 is the equation that the software solves for 3D geometries. In lower-dimensional and axisymmetric cases, restrictions on the coordinate dependence mean that the equations differ from case to case. Here is a brief summary of the situation.

which inserted in Equation 2-16 gives

The out-of-plane wave number kz can be set on the Pressure Acoustics page. By default its value is 0. In the mode analysis study −ikz is used as the eigenvalue λ.

For 2D axisymmetric geometries the independent variables are the radial coordinate r and the axial coordinate z. The only dependence allowed on the azimuthal coordinate φ is through a phase factor,

where m denotes the azimuthal mode number. The mode number defines an azimuthal wave number km = m/r. Because the azimuthal coordinate is periodic, m must be an integer. Just like kz in the 2D case, m can be set in the Settings window for Pressure Acoustics.

As a result of Equation 2-18, the equation to solve for the acoustic pressure in 2D axisymmetric geometries becomes

where both the azimuthal wave number km and the axial wave number kz, appear as parameters.

The equation for the 1D case is obtained by letting the pressure depend on a single Cartesian coordinate x:

The eigenvalue λ introduced in this equation is related to the eigenfrequency f, and the angular frequency ω, through λ = i2πf = iω. Because they are independent of the pressure, the solver ignores any dipole and monopole sources unless a coupled eigenvalue problem is being solved.

Equation 2-19 applies to the 3D case. The equations solved in eigenfrequency studies in lower dimensions and for axisymmetric geometries are obtained from their time-harmonic counterparts, given in the previous subsection, by the substitution ω2 → −λ2.

See Mode Analysis Study in the Pressure Acoustics, Boundary Mode Equations section. The mode analysis study type is only available for the Pressure Acoustics, Frequency Domain interface in 2D and 1D axisymmetric components, where the solver solves for the eigenvalues λ = −ikz for a given frequency. Here kz is the out-of-plane wave number of a given mode and the resulting pressure field p represents the mode on the cross section of an infinite waveguide or duct.