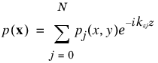When an acoustic wave of a given angular frequency ω is fed into a waveguide or a duct, only a finite set of shapes, or modes, for the transverse pressure field can propagate over long distances inside the structure. The higher the frequency, the higher the number of sustainable modes.

Take, as an example, a uniform straight duct whose axis is in the z direction. The acoustic field in such a duct can be written as a sum of the form

The constant kzj is the axial wave number of the jth propagating transverse mode, pj(x, y). These transverse modes and their associated axial wave numbers are solutions to an eigenvalue problem defined on the duct’s cross section. The mode analysis capabilities in The Pressure Acoustics, Boundary Mode Interface makes it possible to solve such eigenvalue problems. The physics interface is available for 3D Cartesian and 2D axisymmetric geometries and solves for the transverse eigenmodes for the acoustic pressure p and the associated propagation constants kz. The Mode Analysis Study is briefly discussed.

The eigenvalue solver computes a specified number of solutions {pj, λj} to the equation

defined on a 2D boundary of the modeling domain (in 3D) or on the 2D domain itself, with λ = −ikn as the eigenvalue. In this equation, p is the in-plane pressure, ρc is the density, cc is the speed of sound, ω is the angular frequency, and kn is the propagation constant in the direction normal to the surface, in this context also referred to as the out-of-plane wave number.

Notice that the above equation is identical to the time-harmonic equation for pressure acoustics, except that kn is interpreted as an eigenvalue and not as a parameter.

For axisymmetric geometries, the relevant eigenvalue equation to solve for the radial pressure modes and the eigenvalues λ is

Here m, the azimuthal mode number, is an integer-valued parameter. The equation is defined on the interval r1 < r < r2. The eigenvalue λ is defined in terms of the axial wave number kz through the equation λ = −ikz.