Add a Background Pressure Field node to model a background/incident pressure wave to study the scattered pressure field
ps, which is defined as the difference between the total acoustic pressure
pt and the background pressure field
pb:
This feature sets up the equations in a so-called scattered field formulation where the dependent variable is the scattered field p =
ps. In a model where the background pressure field is not defined in all acoustic domains (or it is different), continuity is automatically applied in the total field
pt on interior boundaries between domains.
Select a Background pressure field type:
Plane wave (the default),
Cylindrical Wave,
Spherical Wave, or
User defined. For 2D axisymmetric models, it is possible to expand the plane wave in their cylindrical harmonics.
To set up and calculate the intensity variables for the total, background, and scattered acoustic fields, select Calculate background and scattered field intensity at the bottom of the settings window. This requires an additional input of the
Density ρ (SI unit: kg/m
3) for the defined background pressure field. Selecting this option will also define the velocity variables for the various fields. Enabling this is useful for analyzing reflection problems, where the ratio between incident (background) and reflected (scattered) field power is of interest.
The Plane wave option defines the background pressure field
pb of the type:
where p0 is the wave amplitude,
k is the wave vector with amplitude
ks = ω/c and wave direction vector
ek, and
x is the location on the boundary.
For Plane wave enter values for the
Pressure amplitude p0 (SI unit: Pa), the
Speed of sound c (SI unit: m/s) of the fluid defining the field, either
From material or
User defined, enter a
Wave direction ek (dimensionless), and a
Phase ϕ (SI unit: rad).
In 2D axisymmetric models, the incident fields take a slightly different form due to the geometrical restrictions. Only the z-component for the
Wave direction ek can be entered. Per default, the wave can only travel in the axial direction since this is the only axisymmetric form of a plane wave.
By selecting Enable plane wave expansion, the plane wave is expanded in its cylindrical harmonics and a general
Wave direction ek can be selected. This sets up a wave of the form:
where m is the
Azimuthal mode number specified in the
Pressure Acoustics Equation Settings. To expand the solution, it is necessary to run a
Parametric Sweep over the mode number from 0 up to the desired resolution.
The Cylindrical Wave option defines the background pressure field
pb as a predefined cylindrical wave:
where p0 is the amplitude given at the reference distance
rref = 0.548/
ks (the distance where the Hankel function is one),
ks = ω/c is the wave number,
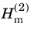
is the Hankel function of the second kind (representing an outgoing cylindrical wave),
rs is the distance from the source axis,
esa is the direction of the source axis,
x0 is a point on the source axis, and
x is the location on the boundary.
For Cylindrical Wave, enter a
Pressure amplitude at reference distance p0 (SI unit: Pa), the
Speed of Sound c (SI unit: m/s) of the fluid defining the field, either
From material or
User defined, enter a
Source Location x0 (SI unit: m), a
Source Axis esa (the vector does not need to be normalized), and a
Phase ϕ (SI unit: rad).
The Spherical Wave option defines the background pressure field
pb as a predefined spherical wave (only for 2D axisymmetric and 3D):
where p0 is the amplitude given at the reference distance of 1 m,
ks = ω/c is the wave number,
rs is the distance from the source,
x0 is the source location of the spherical wave, and
x is the location on the boundary.
For Spherical Wave, enter a
Pressure amplitude at reference distance p0 (SI unit: Pa), the
Speed of Sound c (SI unit: m/s) of the fluid defining the field, either
From material or
User defined, enter a
Source Location x0 (SI unit: m), and a
Phase ϕ (SI unit: rad).
For the User defined option, enter an expression for the
Background pressure field pb (SI unit: Pa).