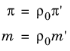The definitions of the piezoresistance and elastoresistance material properties implied by Equation 6-1, Equation 6-2, and Equation 6-8 include the resistivity of the material implicitly. This approach is common in the theoretical literature (see for example Ref. 1 and Ref. 2), since it is essential for a generalized description of the phenomena. However, many engineering texts (see for example Ref. 3, Ref. 4, and Ref. 5) describe the material properties in terms of a relative change in resistivity. In this approach the quantities π′ and m′ are defined such that:

where ρ0 is the scalar resistivity of the undeformed material. Here π′ has the units Pa−1 and m′ is dimensionless. For comparison π has the units ΩmPa−1 and m has units Ωm. Equation 6-10 only applies when the resistivity is isotropic in the unstressed case. Cubic materials, such as silicon, have an isotropic resistivity when unstressed and so can employ this approach. It has the advantage that the piezoresistive material properties do not change with doping level for lightly doped silicon (dopant concentrations of less than approximately 1016 cm−3). In COMSOL Multiphysics the built-in material properties have been implemented so that the dopant number density is added in the interface as a model input and the resistivity and conductivity are computed automatically within the material. These quantities are then included as part of the definitions of π and m. This approach provides the maximum level of flexibility (enabling noncubic materials and nonuniform dopant densities to be straightforwardly modeled), without sacrificing the convenience of the approach usually adopted for cubic materials. When entering custom material properties for materials not present in the library, it is important to remember that the resistivity should be included in the piezoresistance or elastoresistance material properties entered in the material library.