
|
|
•
|
A short version, elbow_bracket_brief, treating the three first analysis types in the above list.
|
|
•
|
A complete version, elbow_bracket, treating all nine analysis types.
|
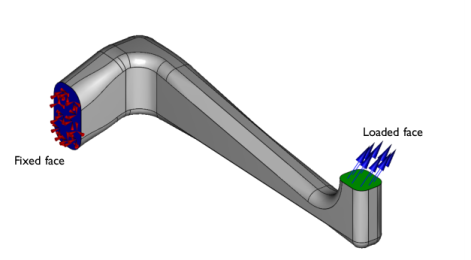
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
Click
|
|
5
|
Browse to the model’s Application Libraries folder and double-click the file elbow_bracket.mphbin.
|
|
6
|
Click
|
|
7
|
|
8
|
Click the
|
|
1
|
|
2
|
On the object fin, select Edges 17, 21, 23, 27, 38, 40, 42, and 44 only.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Solid Mechanics (solid) and choose Fixed Constraint.
|
|
1
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, expand the Study 1 (Static)>Solver Configurations node, then click Solution 1 (sol1).
|
|
2
|
|
1
|
In the Model Builder window, expand the Results>Datasets node, then click Study 1 (Static)/Solution, Static (sol1).
|
|
2
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, under Results>Applied Loads, Static Solution click Boundary Loads (solid).
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, under Study 1 (Static)>Solver Configurations right-click Solution, Static (sol1) and choose Solution>Update.
|
|
1
|
|
2
|
In the Settings window for Global Evaluation, click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Variables>U_max - Maximum deflection - m.
|
|
3
|
Locate the Expressions section. In the table, enter the following settings:
|
|
4
|
Click
|
|
1
|
|
2
|
|
1
|
|
2
|
In the Settings window for Isosurface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Solid Mechanics>Stress>solid.mises - von Mises stress - N/m².
|
|
3
|
|
1
|
|
2
|
|
1
|
|
2
|
In the Settings window for 3D Plot Group, type Static Principal Stress Arrow Plot in the Label text field.
|
|
1
|
In the Static Principal Stress Arrow Plot toolbar, click
|
|
2
|
|
3
|
|
4
|
|
5
|
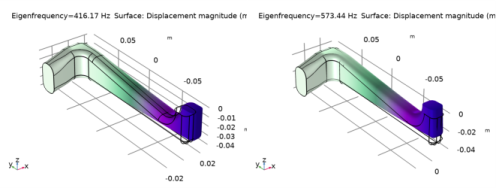
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, expand the Study 2 (Eigenfrequency)>Solver Configurations node, then click Solution 2 (sol2).
|
|
2
|
|
1
|
In the Model Builder window, under Results>Datasets click Study 2 (Eigenfrequency)/Solution, Eigenfrequency (sol2).
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, expand the Results>Undamped Mode Shapes node, then click Results>Export>Animation 1.
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, expand the Study 3 (Damped Eigenfrequency)>Solver Configurations node, then click Solution 3 (sol3).
|
|
2
|
|
1
|
In the Model Builder window, under Results>Datasets click Study 3 (Damped Eigenfrequency)/Solution, Damped Eigenfrequency (sol3).
|
|
2
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, expand the Damped Mode Shapes node, then click Study 2 (Eigenfrequency)>Step 1: Eigenfrequency.
|
|
2
|
|
3
|
|
4
|
In the tree, select Component 1 (Comp1)>Solid Mechanics (Solid)>Linear Elastic Material 1>Damping 1.
|
|
5
|
Click
|

|
1
|
|
2
|
In the Application Libraries window, select Structural Mechanics Module>Tutorials>elbow_bracket_brief in the tree.
|
|
3
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
In the Model Builder window, expand the Study 4 (Time-Dependent)>Solver Configurations>Solution, Time-Dependent (sol4) node, then click Time-Dependent Solver 1.
|
|
4
|
|
5
|
|
6
|
|
7
|
Click to expand the Time Stepping section. Select the Time-step increase delay check box. Keep the default value of 15.
|
|
8
|
|
9
|
|
1
|
|
1
|
In the Model Builder window, expand the Results>Datasets node, then click Study 4 (Time-Dependent)/Solution, Time-Dependent (sol4).
|
|
2
|
|
1
|
|
2
|
In the Settings window for 1D Plot Group, type Time-Dependent Displacement Graphs in the Label text field.
|
|
3
|
|
1
|
|
3
|
In the Settings window for Point Graph, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Solid Mechanics>Displacement>Displacement field - m>u - Displacement field, X component.
|
|
4
|
|
5
|
Select the Description check box.
|
|
6
|
In the associated text field, type X displacement on loaded face.
|
|
1
|
|
2
|
|
3
|
Select the Plot check box.
|
|
4
|
|
1
|
|
1
|
|
2
|
|
1
|
|
2
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click
|
|
6
|
|
1
|
|
2
|
In the Settings window for 3D Plot Group, type Time-Dependent Stress Contour in the Label text field.
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
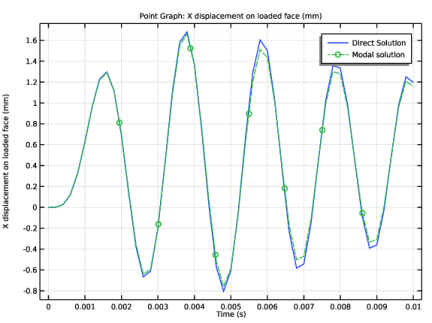
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
4
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Physics and Variables Selection section. Select the Modify model configuration for study step check box.
|
|
5
|
In the tree, select Component 1 (Comp1)>Solid Mechanics (Solid)>Static Load and Component 1 (Comp1)>Solid Mechanics (Solid)>Time-Dependent Load.
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
In the Model Builder window, expand the Study 5 (Modal Time-Dependent)>Solver Configurations>Solution, Modal Time-Dependent (sol5) node, then click Modal Solver 1.
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
Click to expand the Advanced section. In the Load factor text field, type 1+sin(2*pi*500[Hz]*t-pi/2).
|
|
9
|
|
1
|
In the Model Builder window, under Results>Datasets click Study 5 (Modal Time-Dependent)/Solution, Modal Time-Dependent (sol5).
|
|
2
|
|
1
|
|
2
|
In the Settings window for 3D Plot Group, type Modal Time-Dependent Stress Contour in the Label text field.
|
|
3
|
|
1
|
In the Model Builder window, expand the Modal Time-Dependent Stress Contour node, then click Volume 1.
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
Click to expand the Coloring and Style section. Find the Line style subsection. From the Line list, choose Dashed.
|
|
5
|
|
6
|
Locate the Legends section. In the table, enter the following settings:
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Physics and Variables Selection section. Select the Modify model configuration for study step check box.
|
|
5
|
In the tree, select Component 1 (Comp1)>Solid Mechanics (Solid)>Time-Dependent Load and Component 1 (Comp1)>Solid Mechanics (Solid)>Modal Time-Dependent Load.
|
|
6
|
Click
|
|
7
|
|
1
|
In the Model Builder window, expand the Study 6 (Frequency Domain)>Solver Configurations node, then click Solution 6 (sol6).
|
|
2
|
|
1
|
In the Model Builder window, under Results>Datasets click Study 6 (Frequency Domain)/Solution, Frequency Domain (sol6).
|
|
2
|
|
1
|
|
2
|
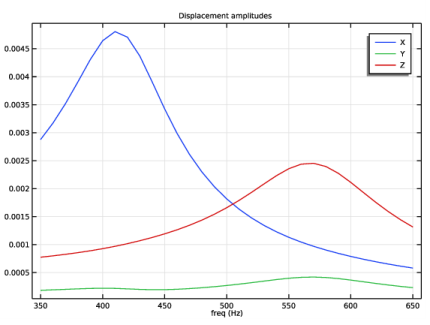
In the Settings window for 3D Plot Group, type Frequency-Response Stress Contour in the Label text field.
|
|
1
|
In the Model Builder window, expand the Frequency-Response Stress Contour node, then click Volume 1.
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
In the Settings window for 1D Plot Group, type Frequency Response Displacement Graphs in the Label text field.
|
|
3
|
|
4
|
|
5
|
|
1
|
|
3
|
In the Settings window for Point Graph, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Solid Mechanics>Displacement>Displacement amplitude (material and geometry frames) - m>solid.uAmpX - Displacement amplitude, X component.
|
|
4
|
|
5
|
|
1
|
|
2
|
In the Settings window for Point Graph, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Solid Mechanics>Displacement>Displacement amplitude (material and geometry frames) - m>solid.uAmpY - Displacement amplitude, Y component.
|
|
3
|
Locate the Legends section. In the table, enter the following settings:
|
|
1
|
|
2
|
In the Settings window for Point Graph, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Solid Mechanics>Displacement>Displacement amplitude (material and geometry frames) - m>solid.uAmpZ - Displacement amplitude, Z component.
|
|
3
|
Locate the Legends section. In the table, enter the following settings:
|
|
4
|
|
1
|
|
2
|
|
3
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Physics and Variables Selection section. Select the Modify model configuration for study step check box.
|
|
5
|
In the tree, select Component 1 (Comp1)>Solid Mechanics (Solid)>Static Load, Component 1 (Comp1)>Solid Mechanics (Solid)>Time-Dependent Load, and Component 1 (Comp1)>Solid Mechanics (Solid)>Modal Time-Dependent Load.
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
In the Model Builder window, expand the Study 7 (Modal Frequency Response)>Solver Configurations>Solution, Modal Frequency-Domain (sol7) node, then click Modal Solver 1.
|
|
4
|
|
5
|
|
6
|
|
1
|
In the Model Builder window, under Results>Datasets click Study 7 (Modal Frequency Response)/Solution, Modal Frequency-Domain (sol7).
|
|
2
|
|
1
|
|
2
|
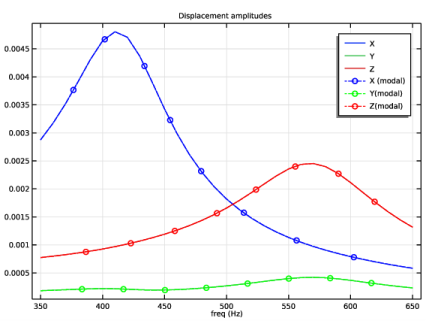
In the Settings window for 3D Plot Group, type Modal Frequency-Response Stress Contour in the Label text field.
|
|
1
|
In the Model Builder window, expand the Modal Frequency-Response Stress Contour node, then click Volume 1.
|
|
2
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Results>Frequency Response Displacement Graphs right-click Point Graph 1 and choose Duplicate.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
Locate the Legends section. In the table, enter the following settings:
|
|
1
|
|
2
|
In the Settings window for Point Graph, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Solid Mechanics>Displacement>Displacement amplitude (material and geometry frames) - m>solid.uAmpY - Displacement amplitude, Y component.
|
|
3
|
|
4
|
Locate the Legends section. In the table, enter the following settings:
|
|
1
|
|
2
|
In the Settings window for Point Graph, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Solid Mechanics>Displacement>Displacement amplitude (material and geometry frames) - m>solid.uAmpZ - Displacement amplitude, Z component.
|
|
3
|
|
4
|
Locate the Legends section. In the table, enter the following settings:
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
|
1
|
|
2
|
|
4
|
|
1
|
|
2
|
|
3
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
In the tree, select Component 1 (Comp1)>Solid Mechanics (Solid)>Static Load, Component 1 (Comp1)>Solid Mechanics (Solid)>Time-Dependent Load, Component 1 (Comp1)>Solid Mechanics (Solid)>Modal Time-Dependent Load, and Component 1 (Comp1)>Solid Mechanics (Solid)>Modal Frequency Load.
|
|
5
|
Click
|
|
6
|
|
1
|
In the Model Builder window, expand the Study 8 (Parametric Static)>Solver Configurations node, then click Solution 8 (sol8).
|
|
2
|
|
1
|
In the Model Builder window, under Results>Datasets click Study 8 (Parametric Static)/Solution, Parametric Static (sol8).
|
|
2
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, expand the Results>Applied Loads, Parametric Solution>Boundary Loads (solid) 1>Gray Surfaces node.
|
|
2
|
|
1
|
|
2
|
|
3
|
Click Yes to confirm.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
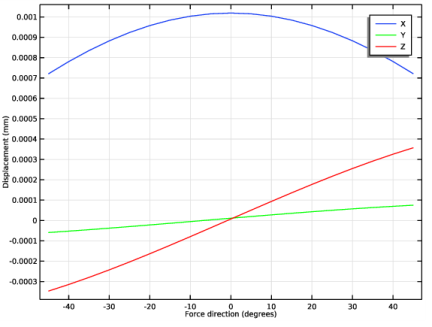
In the associated text field, type Force direction (degrees).
|
|
7
|
|
8
|
In the associated text field, type Displacement (mm).
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Locate the Legends section. In the table, enter the following settings:
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Locate the Legends section. In the table, enter the following settings:
|
|
1
|
|
2
|
|
3
|
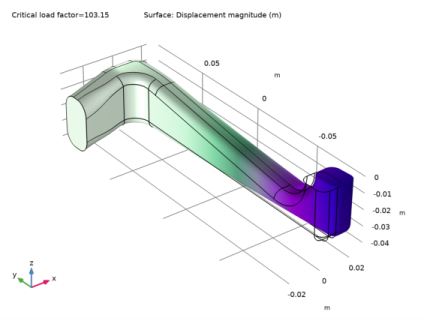
Find the Studies subsection. In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Linear Buckling.
|
|
4
|
|
5
|
|
1
|
|
2
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
In the tree, select
Component 1 (Comp1)>Solid Mechanics (Solid)>Static Load, Component 1 (Comp1)>Solid Mechanics (Solid)>Time-Dependent Load, Component 1 (Comp1)>Solid Mechanics (Solid)>Modal Time-Dependent Load, Component 1 (Comp1)>Solid Mechanics (Solid)>Modal Frequency Load, and Component 1 (Comp1)>Solid Mechanics (Solid)>Parametric Load. |
|
5
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
In the tree, select
Component 1 (Comp1)>Solid Mechanics (Solid)>Static Load, Component 1 (Comp1)>Solid Mechanics (Solid)>Time-Dependent Load, Component 1 (Comp1)>Solid Mechanics (Solid)>Modal Time-Dependent Load, Component 1 (Comp1)>Solid Mechanics (Solid)>Modal Frequency Load, and Component 1 (Comp1)>Solid Mechanics (Solid)>Parametric Load. |
|
5
|
Click
|
|
6
|
|
1
|
In the Model Builder window, expand the Study 9 (Linear Buckling)>Solver Configurations node, then click Solution 9 (sol9).
|
|
2
|
|
1
|
In the Model Builder window, under Results>Datasets click Study 9 (Linear Buckling)/Solution, Linear Buckling (sol9).
|
|
2
|
|
1
|
In the Model Builder window, under Results>Datasets click Study 9 (Linear Buckling)/Solution Store 1 (sol10).
|
|
2
|
|
1
|
|
2
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
In the tree, select
Component 1 (Comp1)>Solid Mechanics (Solid)>Time-Dependent Load, Component 1 (Comp1)>Solid Mechanics (Solid)>Modal Time-Dependent Load, Component 1 (Comp1)>Solid Mechanics (Solid)>Modal Frequency Load, Component 1 (Comp1)>Solid Mechanics (Solid)>Parametric Load, and Component 1 (Comp1)>Solid Mechanics (Solid)>Buckling Preload. |
|
5
|
Click
|
|
1
|
|
2
|
|
3
|
In the tree, select
Component 1 (Comp1)>Solid Mechanics (Solid)>Modal Time-Dependent Load, Component 1 (Comp1)>Solid Mechanics (Solid)>Modal Frequency Load, Component 1 (Comp1)>Solid Mechanics (Solid)>Parametric Load, and Component 1 (Comp1)>Solid Mechanics (Solid)>Buckling Preload. |
|
4
|
Click
|
|
1
|
In the Model Builder window, under Study 5 (Modal Time-Dependent) click Step 1: Time Dependent, Modal.
|
|
2
|
In the Settings window for Time Dependent, Modal, locate the Physics and Variables Selection section.
|
|
3
|
In the tree, select Component 1 (Comp1)>Solid Mechanics (Solid)>Modal Frequency Load, Component 1 (Comp1)>Solid Mechanics (Solid)>Parametric Load, and Component 1 (Comp1)>Solid Mechanics (Solid)>Buckling Preload.
|
|
4
|
Click
|
|
1
|
|
2
|
|
3
|
In the tree, select Component 1 (Comp1)>Solid Mechanics (Solid)>Modal Frequency Load, Component 1 (Comp1)>Solid Mechanics (Solid)>Parametric Load, and Component 1 (Comp1)>Solid Mechanics (Solid)>Buckling Preload.
|
|
4
|
Click
|
|
1
|
In the Model Builder window, under Study 7 (Modal Frequency Response) click Step 1: Frequency Domain, Modal.
|
|
2
|
In the Settings window for Frequency Domain, Modal, locate the Physics and Variables Selection section.
|
|
3
|
In the tree, select Component 1 (Comp1)>Solid Mechanics (Solid)>Parametric Load and Component 1 (Comp1)>Solid Mechanics (Solid)>Buckling Preload.
|
|
4
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
Click
|