The Linearized Navier–Stokes, Frequency Domain (lnsf) interface (), found under the Acoustics>Aeroacoustics branch () when adding a physics interface, is used to compute the acoustic variations in pressure, velocity, and temperature in the presence of any stationary isothermal or nonisothermal background mean flow. The physics interface is used for aeroacoustic simulations that can be described by the linearized Navier–Stokes equations.

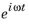
The equations defined by the Linearized Navier–Stokes, Frequency Domain interface are the linearized continuity, momentum (Navier–Stokes), and energy equations. The physics interface solves for the acoustic variations in the pressure p, velocity field u, and temperature T. The harmonic variation of all fields and sources is given by using the +iω convention. The equations are formulated in the frequency domain for any fluid including losses due to viscosity and thermal conduction. The background mean flow can be any stationary flow.

The Linearized Navier–Stokes, Frequency Domain interface is formulated in the so-called scattered-field formulation where the total acoustic field (subscript t) is the sum of the scattered field (the field solved for p, u, and T) and a possible background acoustic field (subscript “b”), such that

All governing equations and boundary conditions are formulated in the total field variables. When no Background Acoustic Fields feature is present (the background field values are zero per default) the total field is simply the field solved for

Coupling the interfaces to structures enables detailed vibration analysis of structures in the presence of flow, such as FSI in the frequency domain. The coupling in the frequency domain and time domain is readily performed using the predefined Aeroacoustic-Structure Boundary multiphysics coupling feature.

Coupling between a background mean flow, computed from a Fluid Flow model, and the Linearized Euler model is handled by the Background Fluid Flow Coupling multiphysics coupling and the dedicated Mapping study. Details are also found in the Mapping Between Fluid Flow and Acoustics Mesh section

When this physics interface is added, these default nodes are also added to the Model Builder — Linearized Navier–Stokes Model, Wall, and Initial Values. For axisymmetric components, an Axial Symmetry node is also added.

Then, from the Physics toolbar, add other nodes that implement, for example, boundary conditions and sources. You can also right-click Linearized Navier–Stokes, Frequency Domain to select physics features from the context menu.

The Label is the default physics interface name.

The Name is used primarily as a scope prefix for variables defined by the physics interface. Refer to such physics interface variables in expressions using the pattern <name>.<variable_name>. In order to distinguish between variables belonging to different physics interfaces, the name string must be unique. Only letters, numbers, and underscores (_) are permitted in the Name field. The first character must be a letter.

The default Name (for the first physics interface in the model) is lnsf.

Expand the Equation section to see the equations solved for with the Equation form specified. The default selection is Equation form is set to Study controlled. The available studies are selected under Show equations assuming.

Click to select Adiabatic formulation to use an adiabatic equation of state and disable the temperature degree of freedom for the linearized Navier–Stokes equations. This formulation is applicable when the thermal losses can be disregarded, this is often the case in liquids like water. In gases, like air, on the other hand the full formulation is necessary. When Adiabatic formulation is selected, all temperature conditions and options are disabled in the user interface.

For all component dimensions, and if required, click to expand the Equation section, then select Frequency domain as the Equation form and enter the settings as described below.

The default Scaling factor Δ is 1/(iω). This value correspond to the equations for a Frequency Domain study when the equations are study controlled. To get the equations corresponding to an Eigenfrequency study, change the Scaling factor Δ to 1. Changing the scaling factor influences the coupling to other physics.

See Sound Pressure Level Settings for the Pressure Acoustics, Frequency Domain interface.

See Typical Wave Speed for the Pressure Acoustics, Frequency Domain interface.

This physics interface defines these dependent variables (fields), the Pressure p, Velocity field u and its components, and Temperature variation T. The name can be changed but the names of fields and dependent variables must be unique within a model.

To display this section, click the Show More Options button () and select Stabilization in the Show More Options dialog box.

Select the Stabilization Method — No stabilization applied, Galerkin least squares (GLS) stabilization (the default), Streamline upwind Petrov-Galerkin (SUPG) stabilization, or Streamline diffusion (legacy method). When stabilization is selected enter a value for the Stabilization constant αstab (dimensionless). The default value is 1 and is well suited for most modeling situations.

The default GLS stabilization is the most efficient stabilization method as it operates on the convective, reactive, and diffusive parts of the governing equations. This is also the default method and the method suggested for most applications. The stabilization constant αstab can be tuned depending on the problem solved, the nature of the background mean flow, and on the computational mesh.

Note that, if a problem is solved where no background mean flow is present, it is recommended to either use one of the Thermoviscous Acoustics Interfaces or turn off stabilization and switch to a P1-P2-P2 discretization.

From the list select the element order and type (Lagrange or serendipity) the default is Linear for all the dependent variables.