The Grating and Cross Grating features are boundary conditions that release rays into one or more diffraction orders whenever a ray hits a boundary. In reality, the grating surface is a periodic substructure in which the unit cells can be smaller than the electromagnetic wavelength, but the substructure geometry is not explicitly modeled as part of the ray optics simulation. Based on the unit cell size and wavelength, rays that hit the grating will propagate into specific directions (the diffraction orders) in which waves from neighboring unit cells would constructively interfere.

Consider an electromagnetic wave incident on the grating or cross grating surface with vacuum wavelength λ0 (SI unit: m). It therefore has angular frequency ω = 2π/λ0 (SI unit: rad/m). Assuming the surrounding media are transparent or weakly absorbing, the ray propagates in the direction of its wave vector k (SI unit: rad/m) which has magnitude k = ωn/c. Here n (dimensionless) is the absolute refractive index of the material and c = 299,792,458 m/s is the speed of light in a vacuum.

The effect of a grating is to offset the in-plane components of the wave vector by an integer multiple of the reciprocal lattice vector G (SI unit: rad/m), given by

Here d (SI unit: m) is the grating constant, i.e. the width of each unit cell of the periodic substructure; and Tg (dimensionless) is a unit vector that lies in the grating surface and indicates the direction of periodicity. By definition, Tg is orthogonal to the surface normal ns.

The wave vector k of the incident ray can be treated as the vector sum of two constituent vectors, one parallel to the surface (kp) and one perpendicular to it (kn):

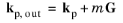
where m (dimensionless) is an integer known as the diffraction order. For m = 0 the ray is specularly reflected if it propagates into the same medium as the incident ray, or refracted (as in Snell’s law) if it propagates into the medium on the opposite side of the grating. The diffraction order m can be any integer but (as detailed in a later section) rays of a given diffraction order can only propagate if the out-of-plane wave vector component remains real-valued while the in-plane component satisfies Equation 3-14.

In a Cross Grating, the in-plane component of the wave vector is offset by integer multiples of two different reciprocal lattice vectors corresponding to two directions of periodicity in the grating surface,

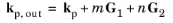
where m and n are the diffraction order numbers. The two reciprocal lattice vectors G1 and G2 (SI unit: rad/m) are defined as

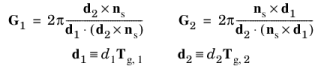
where d1 and d2 (SI unit: m) are the dimensions of one unit cell in the two-dimensional periodic substructure, and Tg,1 and Tg,2 (dimensionless) are unit vectors indicating the corresponding directions of periodicity.

Note that Tg,1 and Tg,2 are not required to be perpendicular to each other, but they cannot be parallel or antiparallel. By definition, both Tg,1 and Tg,2 are orthogonal to the surface normal ns. For the simplified case where Tg,1 and Tg,2 are perpendicular, Equation 3-16 simplifies to

Similar to a grating with a single direction of periodicity, the two diffraction orders m and n can take on any integer values, but that diffraction order can only propagate if the out-of-plane wave vector component can be real-valued while the in-plane component satisfies Equation 3-15.

The magnitude of the outgoing perpendicular component of the reflected and transmitted wavefront can be found from the requirement that the magnitude of the outgoing wave vector kout is equal to the wave number; that is, ||kout|| = k0n, where k0 = ω/c is the wave number in free space. The projections of the reflected and transmitted wave vectors onto the surface normal kn,r and kn,t therefore have magnitudes

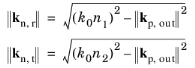
where n1 and n2 are the refractive indices on the incoming (reflected) and outgoing (transmitted) side of the grating, respectively. The outgoing reflected and transmitted wave vectors kr and kt are therefore given by

for rays on the outgoing side (transmitted rays). Each is equivalent to requiring one of the square roots in Equation 3-17 to return a positive real value.

For the Grating (but not the Cross Grating) it is possible to specify relative diffraction order numbers instead of absolute orders. This is particularly useful for blazed gratings.

In a blazed grating, the main detail of the grating microstructure is an array of facets that make an angle θB (SI unit: rad) with respect to the grating normal. This angle is known as the blaze angle. The absolute order number m in which maximum diffraction efficiency occurs can be found from the general grating equation

where the angles α and β (SI unit: rad) are defined as

where θ and γ are the angles of incidence with respect to the grating normal in-plane and out-of-plane respectively. At the peak of the blaze function the angle of diffraction with respect to the grating normal (θ') is equal to θ. Therefore, for any given wavelength λ, the absolute order number is given by

where Δm is the order number relative to the order in which this wavelength is closest to the blaze peak. The in-plane and out-of-plane angles can be derived from the incoming wave vector components. First, we have the component in the direction of the grating normal

where kp is the incoming wave vector projected onto the grating surface. This gives the angle θ and γ as