Glazing Influence on Thermal Performances of a Window

During the design of a building, environmental issues have gained considerable influence in the entire project. One of the first concerns is to improve thermal performances. In this process, simulation software provide key tools for modeling thermal losses and performances in the building

The international standard ISO 10077-2:2012 (Ref. 1) deals with thermal performances of windows, doors, and shutters. It provides computed values of the thermal characteristics of frame profiles in order to validate a simulation software.

COMSOL Multiphysics successfully passes the entire benchmark. This document describes two test cases of ISO 10077-2:2012 related to the glazing influence on thermal performances of a window. Other test cases from this standard are available in the following applications:

•

Thermal Performances of Windows

•

Thermal Performances of Roller Shutters

Figure 1: Geometry of the window and cross-section view.

Model Definition

On each test case, a window section separates a hot internal side from a cold external side. The window frame is the same but in the first application, an insulation panel replaces the traditional glazing. This traditional glazing is tackled in the second application. After solving a model, two quantities are calculated and compared to the normative values:

•

The thermal conductance between internal and external sides

•

The thermal transmittance of the frame is calculated

air cavities

A window frame contains many cavities. The purpose is to ensure thermal insulation. According to the standard, cavities are modeled in different ways depending on their shapes.

The heat flow rate in cavities is represented by an equivalent thermal conductivity keq, which includes the heat flow by conduction, convection, and radiation. It also depends on the geometry of the cavity and on the adjacent materials. The definition of keq is detailed in the next paragraphs.

Cavities are divided into three types:

•

unventilated cavities, completely closed or connected either to the exterior or to the interior by a slit with a width not exceeding 2 mm;

•

slightly ventilated cavities, connected either to the exterior or to the interior by a slit greater than 2 mm but not exceeding 10 mm;

•

well-ventilated cavities, corresponding to a configuration not covered by one of the two preceding types, it is assumed that the whole surface is exposed to the environment so that boundary conditions are applied to (see the Boundary conditions section below for more information).

Unventilated Rectangular Cavity

For an unventilated rectangular cavity, the equivalent thermal conductivity is defined by:

where d is the cavity dimension in the heat flow rate direction, and R is the cavity thermal resistance given by:

Here, ha is the convective heat transfer coefficient, and hr is the radiative heat transfer coefficient. These coefficients are defined by:

where:

•

C1 = 0.025 W/(m·K)

•

C2 = 0.73 W/(m2·K)

•

ΔT is the maximum surface temperature difference in the cavity

•

σ = 5.67·10-8 W/(m2·K4) is the Stefan-Boltzmann constant

•

Tm is the average temperature on the boundaries of the cavity

•

E is the intersurface emittance, defined by:

•

ε1 and ε2 are the surface emissivities (both are equal to 0.90 in this model)

•

F is the view factor of the rectangular section, defined by:

•

d is the cavity dimension in the heat flow rate direction

•

b is the cavity dimension perpendicular to the heat flow rate direction

Slightly Ventilated Rectangular Cavities

For a slightly ventilated cavity, the equivalent thermal conductivity is twice that of an unventilated cavity of the same size.

Boundary conditions

The heat flux conditions for internal and external sides are given by the Newton’s law of cooling:

where Text is the exterior temperature (Text = Ti = 20°C for the internal side and Text = Te = 0°C for the external side). The standard defines thermal surface resistance, Rs, which is related to the heat transfer coefficient, h, by:

Internal and external thermal surface resistances are not equal. Moreover, on boundaries linked to the internal side, an increased thermal resistance is used for the edges. Figure 2 explains how to determine boundaries where it should be applied.

Figure 2: Protected boundaries.

If d is greater than 30 mm, b is set to 30 mm. Otherwise, b = d is chosen. Furthermore, two boundaries are considered as adiabatic: the boundary in contact with the wall and the end of the insulation panel or glazing.

Description of the two Applications

Figure 3 and Figure 4 depict the geometry of each application but only a part of the insulation panel or glazing is represented. Unventilated cavities are red-numbered while slightly ventilated cavities are green-numbered. Boundaries with an increased thermal resistance are represented with bold black lines. Adiabatic boundaries in contact with the wall are represented with a striped rectangle.

Application 1: Wood Frame with an Insulation Panel

The first application studies the heat conduction in the wood frame section with an insulation panel. The frame section is made of two wood blocks with a low thermal conductivity of 0.13 W/(m·K). In order to make the contact between these two blocks and to waterproof the window, two ethylene propylene diene monomer (EPDM) gaskets are used. Two other EPDM blocks are arranged on both sides of the insulation panel. The insulation panel has a very low thermal conductivity of 0.035 W/(m·K).

Two cavities are completely closed and are considered as unventilated. The third one is considered as slightly ventilated.

Figure 3: Geometry of the wood frame with an insulation panel.

Application 2: Wood Frame with a Traditional Glazing

The glazing is made of two glass panels with a thermal conductivity of 1.00 W/(m·K). On the frame side of the glazing, a structure made of aluminum, polysulfide, and silica gel is used to block the glass blocks. Their thermal conductivities are 160 W/(m·K), 0.40 W/(m·K), and 0.13 W/(m·K), respectively. The space between the glass panels is filled with a gas whose thermal conductivity is 0.034 W/(m·K) (so this space is not considered as a traditional air cavity).

Figure 4: Geometry of the wood frame with a glazing.

Results and Discussion

Temperature profiles

Figure 5 and Figure 6 show the temperature profiles for each application.

Figure 5: Temperature profile with the insulation panel.

Figure 6: Temperature distribution with glazing.

Quantities of interest

The quantities of interest are the following:

•

The thermal conductance of the entire section L2D given by:

where

is the heat flow rate through the window (in W/m), Te = 0°C is the external temperature and Ti = 20°C is the internal temperature.

•

The thermal transmittance of the frame Uf defined by:

where bp is the visible width of the panel expressed in meters, bf is the projected width of the frame section expressed in meters and Up is the thermal transmittance of the central area of the panel expressed in W/(m2·K).

•

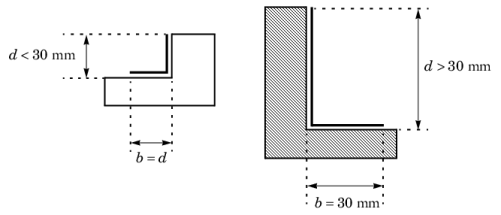
The linear thermal transmittance of the frame Ψ defined by:

where bg is the visible width of the glazing expressed in meters, Ug is the thermal transmittance of the central area of the glazing expressed in W/(m2·K).

Here, Ψ describes the additional heat flow caused by the interaction of the frame and the glass edge, including the effect of the spacer. The thermal transmittance Ug is provided, equal to 1.3 W/(m2·K).

Table 1 and Table 2 compare the numerical results of COMSOL Multiphysics with the expected values provided by ISO 10077-2:2012.

Table 1: comparison between expected and computed values of quantities in Application 1.


Quantity	Expected value	Computed Value	Relative error
L2D (W/(m·K))	0.346	0.345	0.29%
Uf (W/(m2·K))	1.36	1.38	1.47%

Table 2: comparison between expected and computed values of quantities in Application 2.


Quantity	Expected value	Computed Value	Relative error
L2D (W/(m·K))	0.481	0.483	0.42%
Ψ (W/(m2·K))	0.084	0.085	1.19%

The maximum permissible differences to pass this test case are 3% for the thermal conductance and 5% for the (linear) thermal transmittance. The measured values are completely coherent and meet the validation criteria.

Reference

1. European Committee for Standardization, ISO 10077-2:2012, Thermal performance of windows, doors and shutters – Calculation of thermal transmittance – Part 2: Numerical method for frames, 2012.

Heat_Transfer_Module/Buildings_and_Constructions/window_and_glazing_thermal_performances

Modeling Instructions

Root

Start by opening the following prepared file. It already contains global definitions, geometries, local variables, selections, operators and material properties.

From the menu, choose .

Browse to the model’s Application Libraries folder and double-click the file window_and_glazing_thermal_performances_preset.mph.

Window with Insulation Panel

Window with Insulation Panel (comp1)

In the window, expand the node.

Definitions (comp1)

Variables 1

Define the thermal conductance of the section for the postprocessing part as follows.