The Fatigue Module has three strain-based Critical Plane Methods: Smith-Watson-Topper (SWT) Model, Wang-Brown Model, and Fatemi-Socie Model. These types of models are frequently used for low-cycle fatigue modeling.

The most straightforward method is to perform a full elastoplastic analysis and feed the results to the fatigue evaluation. However, this approach can be computationally expensive since the relevant strain input come from a stabilized cycle. With plasticity, due to shake-down or ratcheting, for example, it might be so that several cycles must be computed before such a cycle is obtained.

Smith-Watson-Topper (SWT) is a type of critical plane model where the plane normal to the maximum normal strain range, Δεn, is considered. The model is described by

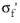
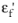
The left-hand side is commonly called the SWT parameter and contains the maximum normal stress during the cycle on the critical plane, σn,max. The right-hand side contains the cycles to failure, Nf, and material parameters , E, b, , and c. At low stresses and strains the fatigue life is limited by a Cycle Cutoff.

The Wang-Brown model is based on finding the plane with maximum shear strain range, Δγ. It contains one extra material parameter, S, which represents the sensitivity to the normal strain range, Δεn, on the critical plane. In reality, S is not a constant but has some dependence on the load level. It is usually of the order 1.0–2.4 for LCF, but it can be as low as 0.3 close to the fatigue limit. The model is described with

where the right-hand side contains the cycles to failure, Nf, and material parameters , E, b, , and c.

Here,  σn,mean is the mean normal stress on the maximum shear plane. It is computed as the average of the maximum and minimum normal stress on the critical plane during the load cycle. At low strains the fatigue life is limited by a Cycle Cutoff.

The Fatemi-Socie model builds on the same ideas as the Wang-Brown model and also considers the plane with the largest shear strain range Δγ. Then, rather than the normal strain, it uses the maximum normal stress during the cycle on the critical plane, σn,max, to model the influence of an opening of the microcrack. In its fundamental form the model is formulated using the fatigue properties for pure shear, something that could be obtained from a torsion test. The Fatemi-Socie relation can be written as

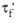
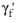
where the right-hand side contains the load cycles to failure, Nf, and material parameters , G, b, , and c. The normal stress sensitivity constant, k, can be set to 1 as an initial approximation. In reality, k is not a constant but has some dependence on the load level. σys0 is the initial yield stress of the material. At low stresses and strains the fatigue life is limited by a Cycle Cutoff.

Neuber’s rule states that for a notch the product of elastically computed stress and strain is equal to the product of the actual, inelastic, stress and strain. Strictly speaking, it is defined only in terms of a uniaxial stress state. In practice, the stress states are often multiaxial, so here Neuber’s rule is expressed with equivalent stresses, σeq, and strains, εeq.

where E is the modulus of elasticity. The parameters K' and n' are material constants of the cyclic response and not the monotonic response obtained from a standard tensile test.

Initially, Equation 3-1 and Equation 3-2 are solved together to obtain the elastoplastic equivalent (in a von Mises sense) stresses and strains. Hoffmann and Seeger (Ref. 1) have developed an algorithm for approximate computation of the stress and strain amplitudes in a multiaxial case. By following the Hencky’s rule and utilizing the generalized notation of the Hooke’s law they obtained following expression for the total elastoplastic strains

where is the Poisson’s ratio, 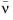is the effective Poisson’s ratio and σ1 and σ2 are the principal stresses. The third principal stress is zero. The expression for the equivalent stress is given by