Critical Plane Methods
For multiaxial cases many of the most popular fatigue criteria are based on the concept of a critical plane. A critical plane is a plane with a certain orientation in a point in the loaded structure that maximizes some stress or strain expression. Different models use different criteria to determine the critical plane. A successful model must be able to predict both the fatigue life and the dominant failure plane. For nonproportional loading the orientation of the critical planes is nontrivial and the loading history needs to be examined for all possible directions in order to find the critical plane.
Selection of Search Directions
The search for a critical plane is generally a computationally heavy task. In each point of the structure for which the fatigue evaluation is to be performed, the worst orientation of a plane must be found. This means that the stress/strain results have to be transformed to a large number of directions.
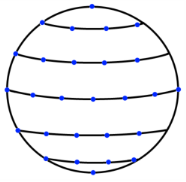
Consider the upper half of the unit sphere. The meridian from the north pole to the equator is subdivided into N equally spaced segments, giving N + 1 points. The length of such a segment is π/2N. From each point a circle of latitude is constructed. This circle is subdivided into M equally sized segments, having approximately the length π/2N. Thus, the number of direction points on each circle of latitude will differ, see Figure 3-6. The total number of normals generated in this manner is approximately 3N2.
Figure 3-6: Search directions for Q = 3.
The accuracy of the algorithm is determined by the spacing of the points, which can be selected by the user as the Search resolution setting Q ( = N + 1) in the Evaluation Settings section for the Strain-Based and Stress-Based nodes.
Finding Maximum Shear Range
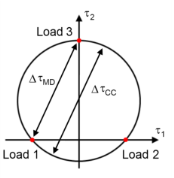
On a given plane the normal stress is a scalar, but the shear stress is a two-dimensional vector. This requires an interpretation of shear stress range, Δτ. For a multiaxial case there is no unique definition of what the maximum shear stress range is. The most strict interpretation is that Δτ is the diameter of the smallest circle that circumscribing the path that the τ vector creates during a load cycle, ΔτCC. This calculation is nontrivial, however, and takes significant computer resources. An alternative is to use the maximum distance between any two points on the path instead, ΔτMD. This simplified procedure could, in extreme cases, underestimate Δτ by 13%. Evaluation of shear range according to both methods is shown in Figure 3-7.
Figure 3-7: Schematic description of methods for evaluation of shear range.
The default method used in the Fatigue Module is to find the circle that circumscribe all points in the shear stress plane. Note that the smallest circumscribing circle will intersect at least two points. The choice for the simplified method is made using the Shear range search method setting in the Evaluation Settings section for the Strain-Based and Stress-Based nodes.
The discussion above, which is in terms of stresses, applies also to the corresponding strain components for a strain based evaluation.