Thermoviscous Boundary Layer Impedance
The Thermoviscous Boundary Layer Impedance condition adds the losses due to thermal and viscous dissipation in the acoustic boundary layers at a wall. The condition is sometimes known simply as the BLI model. The losses are included in a locally homogenized manner, where the losses are integrated through the boundary layers analytically. The condition is applicable in cases where boundary layers are not overlapping. That is, it is not applicable in a very narrow waveguide (with dimensions comparable to the boundary layer thickness) or on very curved boundaries. Other than that, there are no restrictions on the shape of the geometry. This is in contrast to the Narrow Region Acoustics feature which is applicable only in waveguides of constant cross section, but also applicable for all frequencies, that is, also the very narrow case where boundary layers are overlapping. The thickness of the viscous and thermal boundary layers is given by
where ω is the angular frequency, μ the dynamic viscosity, ρ the density, k the coefficient of thermal conductivity, and Cp the (specific) heat capacity at constant pressure.
The Thermoviscous Boundary Layer Impedance condition adds an impedance-like boundary condition by defining the inward normal velocity -n·v at the boundary in terms of the pressure and its tangential derivatives:
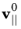
where Tbnd is a possible boundary temperature variation source, vn is a possible normal velocity source, and is a possible tangential velocity source (normal and tangential components are computed from a velocity vector). The expression implemented is a generalization of the expression presented in Ref. 53 including boundary temperature and velocity sources. Velocity sources are presented in Ref. 54 but without including the thermal effects. The general idea of the boundary layer impedance formulation can be found in Pierce, Ref. 5 (see equation 10-4.12 in section 10-4 about the Acoustic Boundary-Layer Theory).
The boundary layer impedance is used in the tutorial Piezoelectric MEMS Speaker. Application Library path: Acoustics_Module/Electroacoustic_Transducers/piezo_mems_speaker
Model Input
Enter a value for the (equilibrium or boundary) Temperature T (SI unit: K). This field is always necessary as the temperature enters the expression for the boundary condition. This corresponds to the equilibrium temperature T0 in the thermoviscous interfaces.
Coordinate System Selection
Select a Coordinate system: Global coordinate system (default) or Boundary boundary System 1 (sys1). If more coordinate systems are present in the model they will also show in the list. The option is used for entering the velocity vector.
Mechanical Condition
Select the Mechanical condition that applies for the wall/boundary: No slip (default), Slip, Velocity, or Normal velocity (slip). These options give most of the relevant mechanical conditions that can be set up using the The Thermoviscous Acoustics, Frequency Domain Interface.
•
No slip, default condition at a wall that is not moving.
•
Slip, condition at a wall that is not moving and where the viscous boundary layer effects are disregarded.
•
Velocity, a moving/vibrating wall where the viscous boundary layer effects are taken into account. A pure tangential wall movement will, for example, generate sound. This is not the case in the lossless case.
•
Normal velocity (slip), a moving/vibrating wall where viscous boundary layer effects are disregarded, only the normal component of the wall movement will contribute to the sound generation.
Thermal Condition
Select the Thermal condition that applies for the wall/boundary: Isothermal (default), Adiabatic, or Temperature variation. These options give most of the relevant thermal conditions that can be set up using the The Thermoviscous Acoustics, Frequency Domain Interface.
•
Isothermal, default condition at a solid wall. Since the thermal conductivity of solids are orders of magnitude larger than fluids the isothermal condition for the fluid is a good approximation in most cases.
•
Adiabatic, condition at a wall where the thermal boundary effects are disregarded.
•
Temperature variation, applies a fluctuating temperature condition at the boundary.
Fluid Properties
Select where the Fluid material is taken from. The default is the Boundary material (remember to assign a material to the boundary if this option is used) or select a specific material if desired.
Enter the necessary material properties for the Speed of sound c, Density ρ, Heat capacity at constant pressure Cp, Ratio of specific heats γ, Thermal conductivity k, and the Dynamic viscosity μ. Per default they are taken From material. For User defined enter a value for the property.