Narrow Region Acoustics
The Narrow Region Acoustics node defines a fluid model for viscous and thermal boundary-layer-induced losses in channels and ducts of constant cross section. The losses due to the viscous and thermal dissipation in the acoustic boundary layer are homogenized and smeared on the fluid. This equivalent-fluid model can be used in long tubes of constant cross section (or only in a slowly varying cross section) instead of a fully detailed thermoviscous acoustics model. This type of model has a low computational cost compared to a thermoviscous acoustic model. The models are applicable for all fluids, that is, both gases and liquids. In the case of waveguides of varying thicknesses or in general other structures with curved surfaces, an alternative is to use the Thermoviscous Boundary Layer Impedance condition.
About the Narrow Region Acoustics Models
Duct Properties
Select a Duct type: Wide duct approximation (the default), Very narrow circular duct (isothermal), Slit, Circular duct, Rectangular duct, Equilateral triangular duct, or User defined.
The Slit, Circular duct, Rectangular duct, and Equilateral triangular duct models are applicable as long as the cross-section dimension is much smaller than the wavelength and the boundary layer thickness is smaller than the wavelength. The cross-section parameter can be a slowly varying function of space. These are known as a low reduced frequency (LRF) model.
•
For Wide duct approximation enter a Hydraulic diameter Hd (SI unit: m).
This model can be used in ducts of any cross section as long as the hydraulic diameter of the duct (four times the cross-section area divided by circumference) is much larger than the viscous boundary layer thickness.
•
For Very narrow circular duct (isothermal) enter the duct Radius a (SI unit: m).
This model is only valid for very narrow circular ducts where isothermal conditions apply. The radius of the duct has to be much smaller than the thickness of the thermal boundary layer. For this model it is assumed that the compressibility (bulk modulus) of the fluid also takes the isothermal value.
•
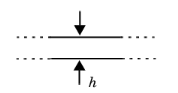
For Slit enter the slit Height h (SI unit: m). Use this model in narrow slit domains to include the damping and attenuation that occurs here because of the losses in the viscous and thermal boundary layer.
•
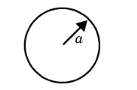
For Circular duct enter the duct Radius a (SI unit: m). This model is useful for modeling the damping and attenuation that occurs when acoustic waves propagate in all tubing systems of small cross-section dimensions.
•
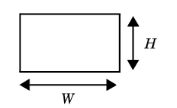
For Rectangular duct enter the duct Side lengths W and H (SI unit: m). Use this model for waveguides and ducts with a rectangular cross section. Also see Advanced Physics Options for additional settings.
•
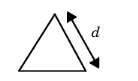
For Equilateral triangular duct enter the duct Side length d (SI unit: m). Use this model for waveguides and ducts with an equilateral triangular cross section.
To determine the complex propagation constants for a waveguide, of arbitrary cross section, use The Thermoviscous Acoustics, Boundary Mode Interface. Apply it on the cross-section geometry of the waveguide. The interface solves for the propagating modes and includes all losses in detail. The complex wave number kc is then given by the plane wave mode solved for. This is the variable tabm.kn. The predefined variable tabm.Zc gives the (lumped) specific characteristic complex impedance Zc. Search for the mode nearest to the (lossless) plane wave mode.
Fluid Properties
Based on your selection in Duct Properties, different fluid properties need to be entered.
For User defined, enter the value for the Complex wave number kc (SI unit: rad/m) and (specific characteristic) Complex acoustic impedance Zc (SI unit: Pa·s/m). These values can be used to model the propagation in ducts of arbitrary cross sections.
For the other duct types, several other fluid properties are needed. The default values for the following are taken From material.
•
Speed of sound c (SI unit: m/s)
•
Density ρ (SI unit: kg/m3)
•
Ratio of specific heats γ (SI unit: 1). In many liquids the value of γ is close to 1, the exact value can be derived from the expression where the (isobaric) coefficient of thermal expansion αp and the isothermal compressibility βT is used.
•
Dynamic viscosity μ (SI unit: Pa·s)
The following are available for Wide duct approximation, Slit, Circular duct, Rectangular duct, and Equilateral triangular duct:
•
Heat capacity at constant pressure Cp (SI unit: J/(kg·K))
•
Thermal conductivity k (SI unit: W/(m·K))
Advanced Physics Options
To display this section, click the Show More Options button (), select Advanced Physics Options and choose Rectangular duct as the Duct type.
The Number of terms for the sum N (used to describe the rectangular duct model) can be set. The default is N = 100 and should cover most cases, see under Slits, Circular Ducts, Rectangular Ducts, and Equilateral triangular Ducts.
•
Lumped Receiver Connected to Test Setup with a 0.4-cc Coupler: The Application Library path Acoustics_Module/Electroacoustic_Transducers/lumped_receiver_04cc
•
Generic 711 Coupler — An Occluded Ear-Canal Simulator: The Application Library path Acoustics_Module/Tutorials,_Thermoviscous_Acoustics/generic_711_coupler
The Narrow Region Acoustics models are so-called equivalent fluid models that have a non-trivial (nonlinear) dependency on the frequency. This means that performing an eigenfrequency analysis should be considered carefully, see Eigenfrequency Study. Moreover, the linearization process (linearization with respect to the frequency) of the underlying mathematical models can cause numerical problems (an error message is thrown). For the Rectangular duct one remedy is to decrease the number of terms used in the sum, for the Circular duct it can be necessary to switch to another model, like the Very narrow circular duct (isothermal).