In 2D geometries, the temperature is assumed to be constant in the out-of-plane direction (z direction with default spatial coordinate names). The equation for heat transfer in solids, Equation 4-14, and in fluids, Equation 4-16, are replaced by:

Here dz is the thickness of the domain in the out-of-plane direction. Here, the conductive heat flux, q, becomes

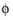
In 1D axisymmetric geometries, the temperature is assumed to be constant in the out-of-plane direction (z direction with default spatial coordinate names) in addition to the axisymmetry (-coordinate with default spatial coordinate names). The equation for heat transfer in solids, Equation 6-15 is replaced by

where dz is the thickness of the domain in the z direction. The equation for heat transfer in fluids, Equation 6-5, is replaced by

Here, the conductive heat flux, q, becomes

In 1D geometries, the temperature is assumed to be constant in the radial direction. The equation for heat transfer in solids, Equation 6-15 is replaced by

where Ac is the cross section of the domain in the plane perpendicular to the 1D geometry. The equation for heat transfer in fluids, Equation 6-5, is replaced by

Here, the conductive heat flux, q, becomes

Out-of-plane flux conditions would apply to the exterior boundaries of the domain if the 1D geometry was seen as a cylinder. With the geometry reduction process, this heat flux condition is mathematically expressed using the cross section perimeter, Pc, as in:

where q0, z is the heat flux density distributed along the cross section perimeter.