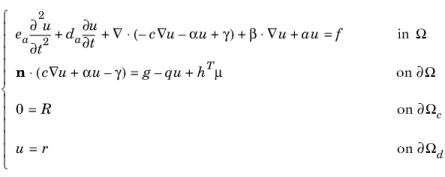Many PDEs originating from physics interfaces and other fields can be cast into a generic form containing derivatives up to second order in both time and space but no mixed derivatives. In COMSOL Multiphysics, you can define a PDE of this type by specifying coefficients for the derivatives of different orders. This results in a coefficient form PDE, which for one dependent variable u reads:

The first line (equation) of Equation 16-2 is the PDE, which must be satisfied in Ω. The second and third equations are the boundary conditions, which must hold on ∂Ω. The second equation is a generalization of a Neumann boundary condition. The third equation is a general constraint, with a Dirichlet boundary condition as a special case. For more information about the boundary conditions, see The General Form PDE.

To define a PDE on coefficient form in one of the PDE interfaces, you specify the coefficients c, α, γ, β, and a and the boundary terms f, g, R, and r. They can all be functions of the spatial coordinates as well as of dependent variables and other predefined or user-defined variables and parameters. A PDE is guaranteed to be linear when the coefficients vary only with the spatial coordinates (or are constants). A PDE is nonlinear if the c, α, β, a, h, or q coefficients depend on u or its derivatives (for example, the components of ∇u), or if γ, f, g, R, or r are nonlinear in u.

For a single dependent variable u, all the coefficients in the above equation are scalars except α, β, and γ, which are vectors with n components. The coefficient c may be given alternatively as a scalar or an n-by-n matrix to model anisotropic materials. When the coefficient form is used for modeling a system of equations, the coefficients are extended with additional vector and matrix dimensions referring to the dependent variable index. See further Multiple Dependent Variables — Equation Systems.

Comparing Equation 16-2 to Equation 16-1 shows that the coefficient form is just a special case of the general form. Applying the following substitutions in the general form, Equation 16-1, turns it into the coefficient form:

The PDE formulations in COMSOL Multiphysics can model a variety of problems, but this guide, as well as the interface, uses descriptive names for the coefficients that fall within the realm of continuum mechanics and mass transfer. For the coefficient form PDE:

Many classical PDEs are instances of the coefficient form PDE. The classical PDEs have their own interfaces, which are found under the Mathematics>Classical PDEs branch () when adding an interface. Table 16-1 shows the available classical PDEs using two notations: the compact notation of vector analysis (used in this documentation) and an expanded component notation.