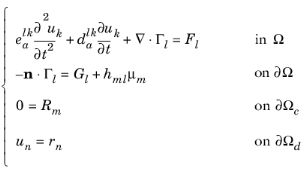In the case of several dependent variables u1,
u2, …,
uN, a general form system of equations takes the following form:
The equation index l and
k ranges from
1 to
N, while the general constraint index
m ranges from
1 to
Mc and the Dirichlet condition index
n ranges from 1 to
Md. The total number of constraints is therefore
M = Mc+Md. This discussion uses the summation convention.
Fl,
Gl,
Rm, and
rn are scalars, whereas
Γl is a spatial vector. The mass and damping coefficients
ea and
da are
N-by-
N matrices, while the constraint force Jacobian h is an
M-by-
N matrix. Note that there are several Lagrange multipliers:
μ1,
μ2,…,
μM.
For a more compact form, let u be a vector with components
uk, let
Γ be a matrix with components
Γlj, and so on. Then the system of equations takes on the same form as given in
Equation 16-1 for a single dependent variable.
It is also possible to write the system entirely on component form, where Γlj are components of the vector
Γl, and
nj components of the normal vector
n. Then the system of equations becomes:
The coefficient form of an equation system with N dependent variables
u1,
u2, …,
uN can be easily obtained from the general form PDE shown in
Equation 16-4 using the substitutions:
Where index k and
l run over dependent variables form 1 to
N, while index
i and
j run over space dimensions from 1 to
K. This means that for the case of a system of equations with
N dependent variables in
K space dimensions, the coefficients have the following sizes:
With two dependent variables u1 and
u2, the stationary PDE problem in coefficient form results in the following equation system:
where u = (u1, u2). The mass term is defined as
However, if ea = 0, then
da is often called the mass coefficient.
Here the third index, k, of
αijk corresponds to the space coordinate suffixes
x and
y.
Here the second index, j, of
γij denotes the space coordinate suffixes for
x and
y.
The normal vector n = (nx, ny) operates on the flux vector in the same way as the divergence operator as explained earlier. If
h has full rank (as in the default identity matrix, for example) only the constraints from the Dirichlet condition are active.