You are viewing the documentation for an older COMSOL version. The latest version is
available here.
where fc can be a constant value (for perfectly plastic materials), or a variable for strain-hardening materials. The yield surface
F is a surface in the space of principal stresses, in which the elastic regime (
F ≤ 0) is enclosed.
For brittle materials, the yield surface represents a failure surface, which is a stress level at which the material collapses instead of deforms plastically.
|
|
Some authors define the yield criterion as f ( σ) = fc, while the yield surface is an isosurface in the space of principal stresses F = 0, which can be chosen for numerical purposes as  .
|
For isotropic plasticity, the plastic potential Qp is written in terms of at most three invariants of Cauchy’s stress tensor
(3-26)

The trace of the incremental plastic strain tensor, which is called the volumetric plastic strain rate 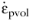
, is only a result of dependence of the plastic potential on the first invariant
I1(
σ), since
∂J2/∂σ and
∂J3/∂σ are deviatoric tensors
A common measure of inelastic deformation is the effective plastic strain rate, which is defined from the plastic shear components
(3-27)
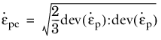
where σys is the yield stress. The scalar function
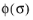
is called effective stress. The default form of the effective stress is the
von Mises stress, which is often used in metal plasticity:
Other expressions can be defined, such as Tresca stress,
Hill orthotropic plasticity,
or a user defined expression.
the effective (von Mises) stress σmises, or other invariants, principal stresses, or stress tensor components.
where σys is the
yield stress level (yield stress in uniaxial tension).
By using the representation of principal stresses in term of the invariants J2 and the Lode angle 0
≤ θ ≤ π/3, this criterion can alternatively be written as
The maximum shear stress is reached at the meridians (θ =
0 or
θ =
π/3). The Tresca criterion can be circumscribed by setting the Lode angle
θ =
0, or equivalently, by a von Mises criterion
The minimum shear is reached at θ =
π/6, so the Tresca criterion can be inscribed by setting a von Mises criterion
When dealing with soils, the parameter k is also called
undrained shear strength.
|
|
The Tresca effective stress, σtresca = σ1 − σ3, is implemented in the variable solid.tresca, where solid is the name of the physics interface node.
|
The von Mises and Tresca criteria are independent of the first stress invariant I1 and are mainly used for the analysis of plastic deformation in metals and ductile materials, though some researchers also use these criteria for describing fully saturated cohesive soils under undrained conditions. The von Mises and Tresca criteria belongs to what researchers call
volume preserving or
J2 plasticity, as the plastic flow is independent on the mean pressure.
A key concept for porous plasticity models is the evolution of the relative density, which is the solid volume fraction in a porous mixture. The relative density is related to the porosity (or void volume fraction)
by
Shima and Oyane (Ref. 14) proposed a yield surface for modeling the compaction of porous metallic structures fabricated by sintering. The criterion can be applied for powder compaction at both low and high temperatures. The yield function and associated plastic potential is defined by an ellipsoid in the stress space. The plastic potential
Qp is written in terms of both von Mises effective stress and mean pressure, and it also considers isotropic hardening due to changes in porosity. The plastic potential is defined by
here, σe is the effective stress,
σ0 is the yield stress,
pm is the pressure, and
ρrel is the relative density. The material parameters
α,
γ, and
m are obtained from curve fitting experimental data. Typical material parameter values for copper aggregates are
α =
6.2,
γ =
1.03, and
m =
5.
Gurson criterion (Ref. 15) consists in a pressure dependent yield function to describe the constitutive response of porous metals, this yield function is derived from the analytical expression of an isolated void immersed in a continuum medium. The void volume fraction, or porosity
φ, is chosen as main variable. The yield function and associated plastic potential is not an ellipse in the stress space, as in
Shima-Oyane Criterion, but it is defined in terms of the hyperbolic cosine function. The plastic potential for Gurson criterion reads
here, σe is the effective stress,
σ0 is the initial yield stress,
pm is the pressure, and
φ is the porosity.
Tvergaard and Needleman modified Gurson Criterion for porous plasticity to include parameters to better fit experimental data (
Ref. 16-
17). The resulting criterion is called in the literature Gurson-Tvergaard-Needleman (GTN) criterion. The plastic potential for GTN criterion reads
here, σe is the effective stress,
σ0 is the initial yield stress,
pm is the pressure, and
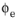
is the effective void volume fraction (effective porosity). Typical correction parameter values are
q1 =
1.5,
q2 =
1.03, and
q3 =
q12.
The effective void value fraction (or effective porosity) 
used in the plastic potential is a function of the current porosity
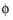
and other material parameters:
Since typical values for the parameters are q3 =
q12, the maximum porosity value is given by
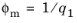
.
The Fleck-Kuhn-McMeeking criterion (Ref. 19), also called FKM criterion, was developed to model the plastic yielding of metal aggregates of high porosity. The yield function and associated plastic potential is derived from expressions for randomly distributed particles. The criterion is considered relevant for aggregates with porosity between 10% and 35%. The plastic potential for FKM criterion reads
here, σe is the effective stress and
pm is the pressure.The
flow strength of the material under hydrostatic loading,
pf, is computed from
here, σ0 is the initial yield stress, and
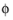
is the void volume fraction (porosity). The maximum void volume fraction
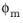
typically takes the value of 36%, the limit of dense random packing of sintered powder.
The FKM-GTN criterion is a combination of the Fleck-Kuhn-McMeeking Criterion and
Gurson-Tvergaard-Needleman Criterion, intended to cover a wider range of porosities (
Ref. 20-
21). The GTN model is used for low void volume fractions (porosity lower than 10%), and for void volume fractions higher than 25%, the FKM criterion is used. In the transition zone, a linear combination of both criteria is used.
Since the relative density is related to the porosity 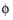 by ρrel
by ρrel =
1 − 
, the change in porosity is also controlled by the change in plastic volumetric strain
here, εN is the mean strain for nucleation,
fN is the void volume fraction for nucleating particles, and
sN is the standard deviation. Typical values for these parameters are
εN =
0.04,
sN =
0.1, and
fN =
0.04. It is assumed that nucleation appears only in tension, and that there is no nucleation in compression.
here, kw is a material parameter,
φ is the current porosity,
nD is a deviatoric tensor coaxial to the stress tensor, and
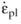
is the plastic strain rate, which depends on the porous plasticity model. The weight
w is computed from stress invariants as
where θ is the Lode angle. The weight variable has a value of
w =
0 at the compressive and tensile meridians (
θ =
0 and
θ =
π/3), and it attains its maximum
w =
1 for
θ =
π/6.
here, τ is the shear stress,
c the cohesion, and

denotes the angle of internal friction.
The Mohr-Coulomb criterion can be written in terms of the invariants I1 and
J2 and the Lode angle 0
≤ θ ≤ π/3 (
Ref. 1,
Ref. 9) when the principal stresses are sorted as
σ1 ≥ σ2 ≥ σ3. The yield function then reads
The tensile meridian is defined when θ =
0 and the compressive meridian when
θ =
π/3.
In the special case of frictionless material, (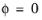 , α
, α =
0,
k =
c), the Mohr-Coulomb criterion reduces to a Tresca’s maximum shear stress criterion,
(σ1 − σ3) =
2k or equivalently
The Mohr-Coulomb criterion causes numerical difficulties when treating the plastic flow at the corners of the yield surface. The Drucker-Prager model neglects the influence of the invariant J3 (introduced by the Lode angle) on the cross-sectional shape of the yield surface. It can be considered as the first attempt to approximate the Mohr-Coulomb criterion by a smooth function based on the invariants
I1 and
J2 together with two material constants (which can be related to Mohr-Coulomb’s coefficients)
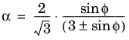 and
and 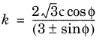
In the special case of frictionless material, (φ =
0,
α =
0,
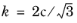
), the Drucker-Prager criterion reduces to the von Mises criterion
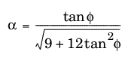 and
and 
 and
and 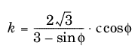
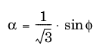 and
and 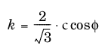
The elliptic cap is an elliptic yield surface of semi-axes as shown in Figure 3-10. The initial pressure
pa (SI units: Pa) denotes the pressure at which the elastic range circumscribed by either a Mohr-Coulomb pyramid or a Drucker-Prager cone is not valid any longer, so a cap surface is added. The limit pressure
pb gives the curvature of the ellipse, and denotes the maximum admissible hydrostatic pressure for which the material starts deforming plastically. Pressures higher than
pb are not allowed
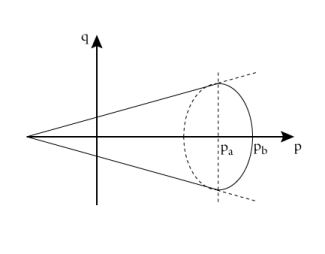
the point (pa,
qa) in the Haigh–Westergaard coordinate system is where the elliptic cap intersects either the Mohr-Coulomb or the Drucker-Prager cone.
here, pb0 is the initial value for the limit pressure
pb,
Kiso is the isotropic hardening modulus,
εpvol the volumetric plastic strain, and
εpvol,max the maximum volumetric plastic strain. Instead of providing the value for the initial pressure
pa (SI units: Pa), the ellipse’s aspect ratio
R is entered.
Note that the volumetric plastic strain εpvol is negative in compression, so the limit pressure
pb is increased from
pb0 as hardening evolves.
Matsuoka and Nakai (Ref. 3) discovered that the sliding of soil particles occurs in the plane in which the ratio of shear stress to normal stress has its maximum value, which they called the
mobilized plane. They defined the yield surface as
where the parameter μ =
(τ/
σn)STP equals the maximum ratio between shear stress and normal stress in the
spatially mobilized plane (STP-plane), and the invariants are applied over the effective stress tensor (this is the Cauchy stress tensor minus the fluid pore pressure).
where I1 and
I3 are the first and third stress invariants respectively, and
k is a parameter related to the direction of the plastic strain increment in the triaxial plane. The parameter
k can vary from 27 for hydrostatic stress conditions (
σ1 =
σ2 =
σ3), up to a critical value
kc at failure. In terms of the invariants
I1,
J2,and
J3, this criterion can be written as
Hill (Ref. 12,
Ref. 13) proposed a quadratic yield function (and associated plastic potential) in a local coordinate system given by the principal axes of orthotropy
ai
(3-28)
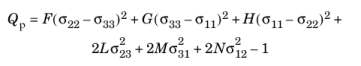
The six parameters F, G, H, L, M, and
N are related to the state of anisotropy. As with isotropic plasticity, the elastic region
Qp < 0 is bounded by the yield surface
Qp = 0.
|
|
Hill plasticity is an extension of J2 (von Mises) plasticity, in the sense that it is volume preserving. Due to this assumption, six parameters are needed to define orthotropic plasticity, as opposed to orthotropic elasticity, where nine elastic coefficients are needed.
|
Hill noticed that the parameters L,
M, and
N are related to the yield stress in shear with respect to the axes of orthotropy
ai, thus they are positive parameters
Here, σysij represents the yield stress in shear on the plane
ij.
The material parameters σys1,
σys2, and
σys3 represent the tensile yield stress in the direction,
a1,
a2, and
a3, and they are related to Hill’s parameters
F,
G, and
H as
(3-29)

Defining Hill’s effective stress as (
Ref. 13)
now depends on the initial yield stress σys0, the hardening function
σh, and the effective plastic strain
εpe.
In the settings for plasticity you specify the effective stress φ(σ) for the yield function from von Mises stress, Tresca stress, Hill effective stress,
or a user defined expression; and
σys0 is the
initial yield stress that defines the onset of plastic deformation.
|
|
When Large plastic strain is selected as the plasticity model for the Plasticity node, either the associate or nonassociated flow rule is applied as written in Equation 3-35.
|
where the yield stress σys(εpe) now depends on the
effective plastic strain εpe.
The yield stress σys(εpe) is then a function of the effective plastic strain and the
initial yield stress σys0
here, the isotropic hardening modulus Eiso is calculated from
For linear isotropic hardening, the isotropic tangent modulus ETiso is defined as (stress increment / total strain increment). A value for
ETiso is entered in the isotropic tangent modulus section for the Plasticity node. The Young’s modulus
E is taken from the parent material (Linear Elastic, Nonlinear Elastic or Hyperelastic material model). For orthotropic and anisotropic elastic materials,
E represents an effective Young’s modulus.
In Ludwik model for nonlinear isotropic hardening, the yield stress σys(εpe) is defined by a nonlinear function of the effective plastic strain. Ludwik equation (also called Ludwik-Hollomon equation) for isotropic hardening is given by the power-law
here, k is the strength coefficient and
n is the hardening exponent. Setting
n = 1 would result in linear isotropic hardening.
here, k is the strength coefficient,
n is the hardening exponent and
ε0 is a reference strain. Noting that at zero plastic strain the initial yield stress is related to the strength coefficient and hardening exponent as
The yield stress σys(εpe) is then defined as
The value of the saturation exponent parameter
β determines the saturation rate of the hysteresis loop for cyclic loading. The
saturation flow stress σsat characterizes the maximum distance by which the yield surface can expand in the stress space. For values
εpe >> 1/β, the yield stress saturates to
where σ∝ is the
steady-state flow stress,
m the saturation coefficient and
n the saturation exponent. For values
mεpen >> 1 the yield stress saturates to
|
|
When Large plastic strain is selected as the plasticity model for the Plasticity node, either the associate or nonassociated flow rule is applied as written in Equation 3-35.
|
Here, σys is the yield stress (which may include a linear or nonlinear isotropic hardening model), and the effective stress
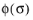
is either the von Mises, Tresca, or Hill stress; or a user defined expression. The stress tensor used in the yield function is shifted by what is usually called the
back stress,
σback.
where the kinematic hardening modulus Ck is calculated from
The value for Ek is entered in the
kinematic tangent modulus section and the Young’s modulus
E is taken from the linear or nonlinear elastic material model. For orthotropic and anisotropic elastic materials,
E represents an averaged Young’s modulus. Note that some authors define the kinematic hardening modulus as
Hk = 2/3Ck.
Armstrong and Frederick (Ref. 7) added memory to Prager’s linear kinematic hardening model. This nonlinear kinematic hardening model allows to capture the Bauschinger effect and nonlinear behavior by non symmetrical tension-compression loading.
here, Ck is the kinematic hardening modulus,
γk is a kinematic hardening parameter, and
εpe the effective plastic strain. Setting
γk = 0 recovers Prager’s rule for linear kinematic hardening.
Chaboche (Ref. 8) proposed a nonlinear kinematic hardening model based on the superposition of
N back stress tensors
each of these back stress tensors σback,i follows a nonlinear Frederick-Armstrong kinematic hardening rule
Practitioners would normally select γk = 0 for one of the back stress equations, thus recovering Prager’s linear rule for that branch
The back stress tensor σback is then defined by the superposition of
N back stress tensors
When small plastic strain is selected as the plasticity model, an additive decomposition is used. If the elastic or plastic strains are large, the additive decomposition might produce incorrect results. As an example, the volume preservation, which is an important assumption in metal plasticity, will no longer be respected. The additive decomposition of strains is however widely used both for metal and soil plasticity.
|
|
When Small plastic strain is selected as the plasticity model for the Plasticity node, and the Include geometric nonlinearity check box is selected on the study Settings window, a Cauchy stress tensor is used to evaluate the yield function and plastic potential. The components of this stress tensor are oriented along the material directions, so it can be viewed as a scaled second Piola-Kirchhoff stress tensor. The additive decomposition of strains is understood as the summation of Green-Lagrange strains.
|
When large plastic strain is selected as the plasticity model, the total deformation gradient tensor is multiplicatively decomposed into an elastic deformation gradient and a plastic deformation gradient.
The flow rule defines the relationship between the increment of the plastic strain tensor

and the current state of stress,
σ, for a yielded material subject to further loading. When
Small plastic strain is selected as the plasticity model for the
Plasticity node, the direction of the plastic strain increment is defined by
Here, λ is a positive multiplier (also called the
consistency parameter or
plastic multiplier), which depends on the current state of stress and the load history, and
Qp is the
plastic potential.
The plastic multiplier λ is determined by the
complementarity or
Kuhn-Tucker conditions
where Fy is the
yield function. The yield surface encloses the elastic region defined by
Fy <
0. Plastic flow occurs when
Fy =
0.
If the plastic potential and the yield surface coincide with each other (Qp =
Fy), the flow rule is called
associated, and the rate in
Equation 3-31 is solved together with the conditions in
Equation 3-30.
(3-31)

For a nonassociated flow rule, the yield function does not coincide with the plastic potential, and together with the conditions in
Equation 3-30, the rate in
Equation 3-32 is solved for the plastic potential
Qp (often, a smoothed version of
Fy).
(3-32)

The evolution of the plastic strain tensor 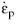
(with either
Equation 3-31 or
Equation 3-32, plus the conditions in
Equation 3-30) is implemented at Gauss points in the plastic element
elplastic.
When Large plastic strain is selected as the plasticity model for the Plasticity node, a multiplicative decomposition of deformation (
Ref. 9,
Ref. 10, and
Ref. 11) is used, and the associated plastic flow rule can be written as the
Lie derivative of the elastic left Cauchy-Green deformation tensor
Bel:
(3-33)
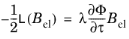
The plastic multiplier λ and the yield function
Φ (written in terms of the Kirchhoff stress tensor
τ) satisfy the Kuhn-Tucker condition, as done for infinitesimal strain plasticity
|
|
The yield function Φ in Ref. 9 and Ref. 10 was written in terms of Kirchhoff stress τ and not Cauchy stress σ because the authors defined the plastic dissipation with the conjugate energy pair τ and d, where d is the rate of strain tensor.
|
The Lie derivative of Bel is then written in terms of the plastic right Cauchy-Green rate
(3-34)
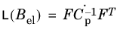
By using Equation 3-33 and
Equation 3-34, the either associated or nonassociated plastic flow rule for large strains is written as (
Ref. 10)
(3-35)
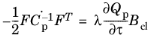
For the associated flow rule, the plastic potential and the yield surface coincide with each other (Qp =
Fy), and for the nonassociated case, the yield function does not coincide with the plastic potential.
(3-37)
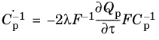
The plastic flow rule is then solved at Gauss points in the plastic element elplastic for the inverse of the plastic deformation gradient
Fp−1, so that the variables in
Equation 3-37 are replaced by
After integrating the flow rule in Equation 3-37, the plastic Green-Lagrange strain tensor is computed from the plastic deformation tensor
|
|
When Large plastic strain is selected as the plasticity model for the Plasticity node, the effective plastic strain variable is computed as the true effective plastic strain (also called Hencky or logarithmic plastic strain).
|
|
|
When either Large plastic strain or Small plastic strain is selected as the plasticity model for the Plasticity node, the out-of-plane shear strain components are not computed in 2D, neither for plane stress nor plane strain assumption.
|
where “old” denotes the previous time step and Λ = λΔt, where
Δt is the pseudo-time step length.
For large plastic strains, Equation 3-37 is numerically solved with the so-called
exponential mapping technique
For each Gauss point, the plastic state variables (εp or
Fp−1, depending on whether small strain or large strain plasticity is selected) and the plastic multiplier,
Λ, are computed by solving either of the above time-discretized flow rules together with the complementarity conditions
|
|
The numerical tolerance to fulfill the condition Fy = 0 is given in SI units of Pascals, and it depends on the initial yield stress (in case of plasticity and porous plasticity) or it is defined in terms of other material parameter (for soil plasticity). This numerical tolerance is 0.1% the value defined in the variable item.tol., where item is the name of the node.
|
As plasticity is rate independent, the plastic dissipation density Wp is obtained after integrating an extra variable in the plastic flow rule.
|
|
When the Calculate dissipated energy check box is selected, the plastic dissipation density is available under the variable solid.Wp and the total plastic dissipation under the variable solid.Wp_tot.
|
