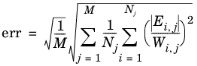Termination Criterion for the Fully Coupled and Segregated Attribute Nodes
You specify the termination criteria in the Settings window for a Fully Coupled or Segregated subnode to the Stationary Solver or the Time-Dependent Solver node. Also see The Segregated Solver (Termination Criterion for a Segregated Solver).
Termination Criterion: Solution
For Termination criterion: Solution, the nonlinear iterations terminate when the following convergence criterion is satisfied: Let U be the current approximation to the true solution vector, and let E be the estimated error in this vector. The software stops the iterations when the relative tolerance exceeds the relative error computed as the following weighted Euclidean norm:
Here M is the number of fields; Nj is the number of degrees of freedom (DOFs) in field j; and Ei,j and Wi,j denote, respectively, the error and weight for the field j and the DOF of index i. Furthermore, the error is defined as the difference between the DOF for the current and the previous iteration, Ei,j = |Ui,j − U'i,j|. You can also express the termination condition as eU < K·TOL, where K is the tolerance factor, and TOL is the relative tolerance. The weights are defined differently for stationary and time-dependent problems. In the former case,
Wi,j = max(|Ui,j|, Sj)
where Sj is a scale factor that the solver determines from the scaling method. You select the scaling method from the Method list in the Scaling section of the Dependent Variables node’s Settings window. The solver then computes the scale factor Sj using the following rules
•
For Automatic, Sj is the average of |Ui,j| for all DOFs i for fixed j, times a factor equal to 10−5 for highly nonlinear problems (that is, where you have selected Automatic highly nonlinear (Newton)) or 0.1 otherwise.
•
For Manual, Sj is the value given in the Scale field. Sj is multiplied by a factor equal to 10−5 for highly nonlinear problems (that is, where you have selected Automatic highly nonlinear (Newton)) or 0.1 otherwise.
•
For Initial-value based, Sj is the average of |Vi,j| for all DOFs i with fixed j times a factor equal to 10−5 for highly nonlinear problems (that is, where you have selected Automatic highly nonlinear (Newton)) or 0.1 otherwise. Here, V = U0 is the solution vector corresponding to the initial value. In case all DOFs are zero for a particular field j, the total mean of |Vi,j| for all i and j is used instead.
•
For None, Wi,j = 1. In this case, err is an estimate for the absolute error.
The (automatically damped Newton) nonlinear solver only checks the convergence criterion if the damping factor for the current iteration is equal to 1. The solver continues as long as the damping factor is not equal to 1 even if the estimated error is smaller than the requested relative tolerance.
For time-dependent problems,
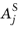
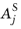
where R is the relative tolerance, is the unscaled absolute tolerance, and is the scaled absolute tolerance for field j. You can specify either of the absolute tolerances or in the Absolute Tolerance section of the Time-Dependent Solver node’s Settings window. If you specify the latter, the scale factor Sj depends on the scaling method selected in the Method list in the Scaling section of the Dependent Variables node’s Settings window:
•
For Automatic, Sj is the average of |Ui,j| for all DOFs i for fixed j when the Update scaled absolute tolerance checkbox is selected. Otherwise, Sj is matrix based and only computed initially.
•
For Manual, Sj is the value given in the Scale field.
•
For Initial-value based, Sj is the average of |Vi,j| for all DOFs i with fixed j, where V = U0 is the solution vector corresponding to the initial value. In case all DOFs are zero for a particular field j, the total mean of |Vi,j| for all i and j is used instead.
•
For None, Sj = 1. In this case, the scaled and unscaled weights are the same.
Termination Criterion: Residual
For Termination criterion: Residual, the nonlinear iterations terminate when the following convergence criterion is satisfied: The software stops the iterations when the relative tolerance exceeds the relative error computed as the weighted Euclidean norm
where F is the current residual. The iterations can also terminate if the relative step size is in the range of a hundred machine epsilon and in addition a full Newton step is taken. In the equation above, the double subscript denotes the degree of freedom index (i) and the field (j) component. You can also express the termination condition as eU <  K·TOL, where K is the tolerance factor, and TOL is the relative tolerance.
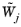
You select a default scaling method from the Method list in the Residual Scaling section of the Dependent Variables node’s Settings window, but can select a different method for each Field or State child node, if desired. The solver then computes the weights using the following rules:
•
For Automatic, the weights are determined considering both the initial residual f0 and the residual after the first iteration f1 as f = 0.5|f0| + 0.5|f1|. 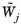is the average of fi, j for all DOFs i for a fixed j. In case all fi, j are zero for that particular field j, the total mean of fi, j for all i and j is used instead.
For time-dependent problems, the first time step calculates the weights 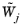based on f as above. Here f is considered as the base residual. In later time steps, the initial residual of the current step f0t and the residual after the first iteration of the current time step f1t will be considered together with the base residual f to determine whether the weights need to be updated for the current time step. The weights are calculated based on f = 0.5|f| + 0.5|f1t| (i = 0 or 1). 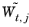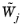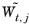The weights are updated as if the ratio / or / for a field j exceeds the threshold defined in the Threshold for updating residual scale field in the settings for a Dependent Variables node or its Field subnodes.
•
For Manual, the weights 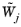is the value given in the Scaling field.
Additional information about the weights for time-dependent problems:
•
With consistent initialization active, the base residual f and the weights 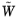will be calculated during the consistent initialization and recalculated after the consistent initialization finishes.
•
When the weights 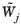for field j need to be updated, then the weights are updated for all fields solved for in the fully coupled solver or in the same segregated step.
•
For wave problems, the weights consist of two parts: the nonvelocity part and the velocity part . The weights are calculated using only the nonvelocity part of the residual f. The weights for the field j are defined to be proportional to the weights as . The proportional ratio r is a fieldwise quantity and is defined as
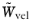
where F is the current residual. The weights are set to be 1 for the first iteration at the first time step. It is updated when the velocity part of the residual is nonzero for the first time. The velocity weights will be updated again when the nonvelocity weights are updated.
Termination Criterion: Solution or Residual
For Termination criterion: Solution or residual, the nonlinear iterations terminate when the relative tolerance exceeds the relative error computed as the minimum of the solution-based error and the error given by the Residual factor times the residual-based error above; that is, when min(eU,βeL) < K·TOL, where K is the tolerance factor, TOL is the relative tolerance, and β is the residual factor.
Termination Criterion: Solution and Residual
For Termination criterion: Solution and residual, the nonlinear iterations terminate the Newton iterations on a solution-based estimated relative error and a residual-based estimated relative error given by the Residual factor times the residual-based error above; that is, when max(eU,βeL) < K·TOL, where K is the tolerance factor, and TOL is the relative tolerance, and β is the residual factor.