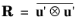
The Elliptic Blending R-ε model belongs to RANS-RSM type of turbulence models and, hence, does not assume a particular form of (the kinematic Reynolds stress tensor). It solves the transport equation for R instead, complemented by the transport equation for the turbulence dissipation rate ε, and by the elliptic equation for the blending variable, which allows to capture the evolution of turbulence structure properly Ref. 36. This leads to more accurate prediction of separation, transient phenomena, effects of swirl and curvature. Moreover, correct description of secondary flows is achieved, which eddy-viscosity based models are intrinsically incapable of. The blending procedure additionally improves the model’s ability to take into account the effect of system rotation and characterize behavior in the near-wall region.

The general framework of Elliptic Blending R-ε is similar to The Turbulent Flow, Wilcox R-ω Interface. The differences are listed below.

The set of Elliptic Blending R-ε model parameters with their default values is

In a rough analogy to The v2-f Turbulence Model, the pressure–strain correlation Πij and the dissipation tensor εij are blended between bulk (homogeneous) and near-wall expressions as

where α is the blending variable.

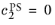
For Elliptic Blending R-ε, the modeling of the homogeneous part of the pressure–strain correlation Πij involves seven model parameters (which is the same as in The SSG-LRR Turbulence Model, although by default)

while the near-wall part of the pressure–strain correlation Πij is

where is n is the normal vector to the nearest wall. Notice that the relations Πkk = 0 and εkk = 2ε still hold.

The ε-equation and α-equation are stated as

The modified coefficient in the ε-equation as well as turbulence length scale and turbulence time scale, are given by

The coefficients and in the turbulent diffusion D are expressed as

In the Elliptic Blending R-ε model, the Simple diffusion option is not allowed for the Reynolds stress diffusion model. The calibration of Hanjalic–Launder, Mellor–Herring, and Lumley relative to Daly–Harlow is made according to Ref. 35. Adjust σk if needed.

For the Low Reynolds Number Wall Treatment, the boundary condition for ε is

where lw is the distance to the closest wall.