The SSG-LRR model belongs to RANS-RSM type of turbulence models and, hence, does not assume a particular form of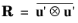 
(the kinematic Reynolds stress tensor). It solves the transport equation for R instead, complemented by the transport equation for the turbulence specific dissipation rate
ω, which allows to capture the evolution of turbulence structure properly
Ref. 34. This leads to more accurate prediction of separation, transient phenomena, effects of swirl and curvature. Moreover, correct description of secondary flows is achieved, which eddy-viscosity based models are intrinsically incapable of.
The set of SSG-LRR model parameters with their default values is
Similar to The SST Turbulence Model the model parameters are blended between
ω-based and
ε-based approaches as
where lw is the distance to the closest wall.
For SSG-LRR the modeling of the pressure–strain correlation Πij involves seven model parameters (after the blending is performed):
The coefficients σ∗ and
τR in the turbulent part of diffusion
D are expressed as
The relation between τR and
σ∗ is based on the correspondence between
Simple diffusion and
Daly–Harlow and follows
Ref. 34. The calibration of
Hanjalic–Launder,
Mellor–Herring, and
Lumley relative to
Daly–Harlow is made according to
Ref. 35. Adjust
D if needed.
.
avoids blending since its value follows from the rapid distortion theory.
