Periodic Structure
To perform a periodic structure calculation, add a Periodic Structure node. The Periodic Structure node has the following default subnodes:
•
Wave Equation, Electric
•
Perfect Electric Conductor
•
Periodic Port
•
Floquet Periodic Condition
•
Reference Direction
By default, two Periodic Port subnodes are added. On the remaining boundaries exterior to the Periodic Structure node, for each pair of parallel boundaries a Floquet Periodic Condition subnode is added.
For standard modeling procedures, there are no settings to make on the Periodic Port and the Floquet Periodic Condition subnodes, as all the settings are made on the Periodic Structure node.
In addition, the following features can be added as subnodes to the Periodic Structure node:
•
Impedance Boundary Condition
•
Layered Impedance Boundary Condition
•
Layered Transition Boundary Condition
•
Perfect Electric Conductor
•
Perfect Magnetic Conductor
•
Transition Boundary Condition
•
Wave Equation, Electric
These subnodes are available from the context menu (right-click the Periodic Structure parent node) or from the Physics toolbar, Attributes menu. For more information about the subnodes listed above, click the respective link.
The selection of the Periodic Structure node defines the periodic unit cell. The reference direction a1 is defined from the selections in the Reference Direction subnode in 3D and from the Excited Port Selection and the Reference Direction subnode selection in 2D. Given the first reference direction a1, the second reference direction a2 is calculated from
,
where a0 is the periodic structure axis direction that is pointing in the direction from the passive port towards the excitation port. Thus, the axis direction equals the normal direction for the excited port.
Given the reference directions, the wave vector for the incident plane wave is given by
,
where k is the material wavenumber at the excitation port and α1 and α2 are the elevation and azimuth angles, respectively. The elevation angle α1 is the angle between the wave vector kinc and the periodic structure axis (kinc⋅a0 ≤ 0, as α1 is in the range from 0 to π/2 radians). For normal incidence, this angle is zero. The azimuth angle α2 is the angle between the first reference direction a1 and the projection of the incident wave vector kinc on the plane spanned by a1 and a2 (the port planes).
In 2D, the elevation angle is simply called the angle of incidence and is denoted α. Furthermore, in the Out-of-Plane Wave Number section of The Electromagnetic Waves, Frequency Domain Interface it is possible to specify an out-of-plane wave vector component kz. Thus, the wave vector of the incident plane wave is given by
From this relation we deduce that
and
.
Here, β is the wave vector component in the axis direction.
The first reference direction a1 also defines the direction of the first primitive vector of the periodic unit cell. That is,
.
The length b1 is obtained from the excited port edges that are aligned with the Excited Port Selection. In 3D, for parallelogram-like unit cells, the second primitive vector b2 is defined from the cell edges that are not parallel to b1. Furthermore, b2 is defined such that
(3-1).
For hexagonal unit cells, three edge vectors are defined from three consecutive hexagon edges:
•
v1 is defined from the hexagon edge that intersects the Reference Direction node edge and point selections.
•
v2 is defined by the hexagon edge that starts where the edge that defines v1 ends.
•
v3 is defined by the hexagon edge that starts where the edge that defines v2 ends.
From these three vectors, the first primitive cell vector is defined by
and the second primitive cell vector is defined from
,
assuming that Equation 3-1 applies. If the cross product does not fulfill Equation 3-1, the expressions for b1 and b2 are swapped.
Domain Selection
The selection is locked to All domains, meaning that the Periodic Structure has the same selection as the The Electromagnetic Waves, Frequency Domain Interface.
Excited Port Selection
Select a boundary that represents or is part of the excited port. The excited port boundary defines the axis a0 of the periodic structure, as the excited port boundary normal and the axis point in the same direction.
To deduce the primitive vectors, the Periodic Structure axis direction should be aligned with one of the Cartesian axes.
Port Handling
This section provides settings to add or remove the passive listener port and to add Diffraction Order subnodes.
•
Clear the Add listener port checkbox to remove the passive listener port.
•
Define the Diffraction order specification — From current parameters or All angles (the default). When From current parameters is selected, clicking the Add Diffraction Orders button, creates Diffraction Order ports that represents propagating waves for the present parameter values. When All angles is selected, clicking the Add Diffraction Orders button, creates Diffraction Order ports that represents propagating waves at least for some angles of incidence. Here, the angle of incidence could be any angle from the incident hemisphere.
•
Define the Refractive index, real part, excited port n1 — From adjacent domain (the default) or User defined. When From adjacent domain is selected, the Refractive index, real part is taken from the domain adjacent to the port. For User defined, enter the Refractive index, real part, excited port n1 (SI unit: 1). The default value is 1.
•
If Add listener port is checked, define the Refractive index, real part, listener port n2 as was done for Refractive index, real part, excited port n1.
When all parameters are defined, click the Add Diffraction Orders button to automatically create Diffraction Order ports as subnodes to all Periodic Port subnodes.
Perform the same action as when clicking the Add Diffraction Orders button, using the COMSOL API, with the Java code
 model.component("comp1").physics("ewfd").feature("ps1").runCommand("addDiffractionOrders");
where “comp1”, “ewfd”, and “ps1” are the tags for the model component, the physics interface, and the periodic structure, respectively, and model is a model object.
Port Mode Settings
Select a Polarization — Linear polarization (default value), Circular polarization, or User defined.
For Linear polarization, select the polarization type — S (default value), P, or Mixed, where S and P represent a polarization orthogonal or parallel to the plane of incidence (spanned by the wave vector for the incident plane wave and the port normal), respectively, and Mixed represents a mixture of S- and P-polarizations. For Mixed Linear polarization also specify the P-polarization power fraction ηP. The default value is 0, meaning that the mode field will be S-polarized.
Fresnel Equations: Application Library path Wave_Optics_Module/Verification_Examples/fresnel_equations
For Circular polarization, select the type of circular polarization — Right-handed (default value) or Left-handed. The convention used here is from the point of view of the source. That is, for right-handed circular polarization, when the thumb points in the direction of wave propagation, the temporal field polarization curls in the direction the right hand fingers. For left-handed circular polarization, the polarization curls temporally along the left hand fingers, when the thumb is pointing in the wave direction.
For User defined Polarization, select an Input quantity — Electric field (default value) or Magnetic field — and define the mode field amplitude for the outgoing wave at the port.
•
For 2D components and if the Input quantity is set to Electric field, define the Electric mode field amplitude. For example, for S-polarization set the x, y, and z components to 0, 0, 1. Similarly, if the Input quantity is set to Magnetic field, define the Magnetic mode field amplitude. For P-polarization, set the x, y, and z components to 0, 0, and 1. The default value is the tangent vector t1. However, if Electric field components solved for, in the Settings for the physics interface, is set to Out-of-plane vector, only the out-of-plane component is nonzero for the Electric mode field amplitude. If Electric field components solved for is set to In-plane vector, only the out-of-plane component is nonzero for the Magnetic mode field amplitude.
In the COMSOL Multiphysics Reference Manual, see the Tangent Variables for more information about the tangent vector t1.
In 2D, define the Angle of incidence α (SI unit: radians), and in 3D define the Elevation angle of incidence α1 (SI unit: radians) and the Azimuth angle of incidence α2 (SI unit: radians).
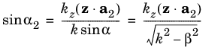Modeling Periodic Structures
Hexagonal Plasmonic Color Filter: Application Library path Wave_Optics_Module/Gratings_and_Metamaterials/hexagonal_plasmonic_color_filter