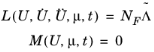
|
1
|
First solves for the initialization problem of the unreduced time-dependent study under some training value of the inputs, and for the initial time t0. This gives an initial value vector V0 (and the first time-derivative vector).
|
|
2
|
Next, the method removes the constraint mode solution and Vd from the initial values. For the constraint mode solution, the training expressions are used for the model inputs.
|
|
•
|
Reduced matrices that can be exported from both the Modal solver and the Modal Reduction solver for both time and frequency domain: the projection matrix P; each column of P is a basis vector.
|
|
•
|
Reduced matrices that can be exported from the Modal solver for both the time domain and the frequency domain: the stiffness matrix Kr, the damping matrix Dr, the damping ratio matrix Dra, the mass matrix Er, the input matrix Br, the time derivative input matrix Brdot, and the second time derivative input matrix Brdotdot. Those matrices are defined in Equation 20-22. The output matrix Cr and the input feedback matrix F defined in Equation 20-27 can also be exported. For the Modal solver, Cr and F are expected to be zero because there are no output variables defined.
|
|
•
|
Reduced matrices that can be exported from the Modal Reduction solver for both the time domain and the frequency domain: All matrices mentioned for Modal solver above can be exported. However, they might not be the full size of the reduced matrix. Rather, it is the submatrix of the full-sized reduced matrix defined in Equation 20-22, which corresponds to all unconstrained reduced DOFs according to the current setting in the Constraint Modes section in a reduced-order model node. The counterparts of those submatrices, which correspond to all constrained reduced DOFs, are denoted as, for example, Krc, Drc, Erc, MAc, MBc, and Mcc. They can also be exported.
|
|
-
|
For the time domain, the reduced load vector l0r (it is L in the reduced matrices list) and Kud defined in Equation 20-22, the initial value vector U0, and the initial derivative vector Udot0. For second-order problems, the initial vector x0 for the state-space system can also be exported.
|
|
-
|
For the frequency domain, the reduced load vector l0r(ω) (it is L in the reduced matrices list) defined in Equation 20-42 for the last given angular frequency ω, the mass matrix times the particular solution PHEVd and the damping matrix times the particular solution PHDVd in Equation 20-44. See also the example below.
|
|
•
|
Vectors that can be exported from the Modal Reduction solver only: constraint modes to inputs map CImap, unconstrained DOF indices to the mode index map DofToMode, and constrained DOF index to that mode index map.
|
|
•
|
Vectors that can be exported from the Modal solver only: All load vectors AllL, which export all load vectors (that is, lor(ω0), lor(ω1),... , lor(ωk)), where ωi corresponds to fi in the Frequencies setting in the Frequency Domain, Modal study.
|
|
•
|
The Modal solver solves the reduced system directly and returns the reconstructed solution. The Modal Reduction solver does not solve the reduced system; instead, it creates a reduced-order model, which represents the reduced system and can be solved in the same way as any other physics. The reduced-order model is a Time Dependent, Modal Reduced-Order Model for time domain, and Frequency Domain, Modal Reduced-Order Model for frequency domain.
|
|
•
|
As indicated by the Exporting the Reduced System section above, the reduced matrices can be exported by both solvers. For the Modal solver, it is in the Output section of the settings for the Modal Solver node. The matrices and vectors are of the full size of the reduced system. For the Modal Reduction solver, you need to go to Results > Derived Values, create a System Matrix node, choose a reduced-order model as the solution, and in the Output section, choose the matrix to output. The matrices and vectors are of eliminated size, which reflects the current setting in the Constraint Modes section in the settings for the reduced-order model node. An exported matrix like Kr is the submatrix of the full-sized reduced matrix, corresponding to all unconstrained reduced DOFs. You can also output the constrained part of the stiffness matrix Krc, which corresponds to the constrained reduced DOFs. If you want to get the full-sized reduced matrices and vectors, then clear all checkboxes in the Constrained column in the Constraint Modes table.
|
|
•
|
|
Modal in the COMSOL Multiphysics Programming Reference Manual.
|