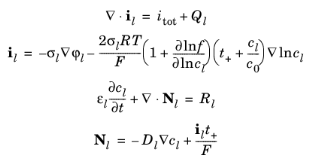The Battery with Binary Electrolyte Interface defines the current balance in the electrolyte, the current balances in the electrodes, the mass balance for a salt, and the mass balance of an intercalating species such as hydrogen in a nickel–metal hydride battery.

The electrolyte in the modeled batteries has to be a quiescent alkaline binary 1:1 electrolyte, containing a cation (Cat+) and an anion (An−).

In the electrolyte and pore electrolyte, two variables are defined: ϕl and cl. Assuming electroneutrality, cl denotes both the Cat+ concentration and the An− concentration.

where il denotes the electrolyte current density, σl the electrolyte conductivity, f the activity coefficient for the salt, t+ the transport number for Cat+ (also called transference number), itot the sum of all electrochemical current sources, c0 the solvent concentration, and Ql denotes an arbitrary electrolyte current source. In the mass balance for the salt, Nl denotes the flux of the cation, εl the electrolyte volume fraction, Dl the electrolyte salt diffusivity, and Rl the total Cat+ source term in the electrolyte.

In the electrode, the current density, is, is defined as

where σs is the electric conductivity.

where Qs is an arbitrary current source term.

Reactions occur on the surface of small solid spherical host particles of radius rp. The reactions can either be electrochemical or chemical adsorption/desorption reactions not involving electrons.

where Θs is a free reaction site and SΘs is an occupied reaction site at the solid particle surface. Additional product species (X, …) are not handled by this physics interface.

with a reaction rate k (SI unit: mol/(s·m2)). The signs νs is here positive, and the reaction rate is defined as positive for reactions going from left to right.

The concentration of Θs does not have to be solved for because the total concentration of reaction sites, cs,max, is assumed to be constant, implying that

An important parameter for intercalation electrodes is the state-of-charge variable soc for the solid particles, defined as

The equilibrium potentials Eeq of intercalation electrodes reactions are typically functions of the soc.

where cs is the concentration of the intercalating species. This equation is solved locally by this physics interface in a 1D extra (pseudo) dimension, using a finite element discretization with the solid phase concentration as dependent variable. The divergence and gradient operator in the above equation are be applied using either spherical, cylindrical, or Cartesian coordinates, depending on the particle type (spheres, cylinders, or flakes).

where Rs,tot is the total surface molar flux of the intercalating species due to the electrochemical and chemical reactions.

where the stoichiometric coefficients, νi, are positive (νox) for products and negative (νred) for reactants in a reduction reaction. From this definition, the number of electrons, n, in the electrode reaction can be calculated according to

where zi denotes the charge of species i.

In the porous electrodes, itot denotes the sum of all charge transfer current density contributions according to

where Av denotes the specific surface. The source term in the mass balance is calculated from

It is also possible to specify additional reaction sources, Rl,src, that contribute to the total species source according to

where the last factor (normally equal to 1) is a scaling factor accounting for differences between the surface area (Av,m) used to calculate the volumetric current density, and the surface area of the particles in the solid lithium diffusion model. Nshape is 1 for Cartesian, 2 for cylindrical, and 3 for spherical coordinates.

The molar source, Rv,tot, due to the electrochemical and chemical reactions at the positive and negative electrodes is given as follows:

A resistive film (also called solid-electrolyte interface, SEI) might form on the solid particles resulting in additional potential losses in the electrodes. To model a film resistance, an extra solution variable for the potential variation over the film, Δϕs,film, is introduced in the physics interface. The governing equation is then according to

where Rfilm (SI unit: Ω·m2) denotes a generalized film resistance. The activation overpotentials, ηm, for all electrode reactions in the electrode then receives an extra potential contribution, which yields

where Y could be some metal deposited on the electrode surface. Because this is not an insertion reaction, cs is of no relevance at this boundary. The stoichiometric coefficients for the above reaction are

where the normal vector n points into the electrolyte domain.

See Cell Capacity and State of Charge in Theory for the Lithium-Ion Battery Interface.

See Defining Initial Cell Charge Distributions Based on Cell Voltage or Cell State of Charge in Theory for the Lithium-Ion Battery Interface.

See Electrolyte Salt Material Balance Formulation in Theory for the Lithium-Ion Battery Interface.

Solving for the logarithm of the salt concentration, lncl, the numerically unstable division by zero is inherently avoided.