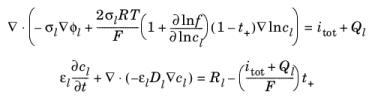COMSOL 6.3 - Theory for the Lithium-Ion Battery Interface

The Lithium-Ion Battery Interface defines the current balance in the electrolyte, the current balances in the electrodes, the mass balance for the lithium salt, and the mass balance of lithium in lithium-ion batteries.

The electrolyte in the modeled batteries has to be a quiescent binary 1:1 electrolyte, containing lithium cations (Li+) and anions (An-).

The physics interface solves for five dependent variables:

•

Δϕs,film, the potential losses due to a resistive film on the electrode particles in the porous electrodes, also called solid-electrolyte interface (SEI),

In the electrolyte and pore electrolyte, two variables are defined, ϕl and cl. Assuming electroneutrality, cl denotes both the Li+ concentration and the An- concentration.

The domain equations in the electrolyte are the conservation of current and the mass balance for the salt according to the following:

where σl denotes the electrolyte conductivity, f the activity coefficient for the salt, t+ the transport number for Li+ (also called transference number), itot the sum of all electrochemical current sources, and Ql denotes an arbitrary electrolyte current source. In the mass balance for the salt, εl denotes the electrolyte volume fraction, Dl the electrolyte salt diffusivity, and Rl the total Li+ source term in the electrolyte.

In the electrode, the current density, is, is defined as

where σs is the electric conductivity.

The domain equation for the electrode is the conservation of current expressed as

where Qs is an arbitrary current source term.

The electrochemical reactions in the physics interface are assumed to be insertion reactions occurring at the surface of small solid spherical particles of radius rp in the electrodes. The insertion reaction is described as

where Θs denotes a free reaction site and LiΘs an occupied reaction site at the solid particle surface.

The concentration of Θs does not have to be solved for since the total concentration of reaction sites, cs,max, is assumed to be constant, implying that

An important parameter for lithium insertion electrodes is the state-of-charge variable for the solid particles, denoted soc. This is defined as

The equilibrium potentials E0 of lithium insertion electrode reactions are typically functions of soc.

The electrode reaction occurs on the particle surface and lithium diffuses to and from the surface in the particles. The mass balance of Li in the particles is described using

where, for Fick’s law, the molar flux Ns is defined as

where cs is the concentration of Li in the solid phase. This equation is solved locally by this physics interface in a 1D pseudo dimension, with the solid phase concentrations at the nodal points for the element discretization of the particle as the independent variables. The gradient is calculated in Cartesian, cylindrical, or spherical coordinates, depending on if the particles are assumed to be best described as flakes, rods, or spheres, respectively.

For the case of Baker–Verbrugge diffusion (Ref. 3), the flux vector is defined as

The boundary conditions are defined as follows:

where RLiΘ denotes the molar flux of lithium at the particle surface, caused by the electrochemical insertion reactions.

The stoichiometric notations used in the physics interface are according to the general electrochemical reaction as expressed below:

where the stoichiometric coefficients, νi, is positive (νox) for products and negative (νred) for reactants in a reduction reaction. From this definition, the number of electrons, n, in the electrode reaction can be calculated according to

where zi denotes the charge of species i. According to these relations, the lithium insertion reaction has the following stoichiometric coefficients:

with a resulting n = 1. These are the default settings for the reactions in this physics interface. When modeling other reactions, such as irreversible anion oxidation or noninsertion solid lithium metal deposition, other coefficients have to be used.

In the porous electrodes, itot, denotes the sum of all charge transfer current density contributions according to

where, Av denotes the specific surface. The source term in the mass balance is calculated from:

It is also possible to specify additional reaction sources, Rl,src, that contribute to the total species source according to

At the surface of the solid particles the following equation applies:

where the last factor (normally equal to 1) is a scaling factor accounting for differences between the surface area (Av,m) used to calculate the volumetric current density, and the surface area of the particles in the solid lithium diffusion model. Nshape is 1 for Cartesian, 2 for cylindrical, and 3 for spherical coordinates.

If the solid phase diffusion coefficient is very large or if the spatial concentration gradients in the particle can be neglected, the solid phase concentration evolution in time can be calculated from

The molar source RvΘ at the positive and negative electrodes is given as follows:

A resistive film (also called solid-electrolyte interface, SEI) might form on the solid particles resulting in additional potential losses in the electrodes. To model a film resistance, an extra solution variable for the potential variation over the film, Δϕs,film, is introduced in the physics interface. The governing equation is then according to

where Rfilm (SI unit: Ω·m2) denotes a generalized film resistance. The activation overpotentials, ηm, for all electrode reactions in the electrode then receives an extra potential contribution, which yields

For a fully relaxed battery cell (at open circuit), the cell voltage Ecell (V) equals the difference between the relaxed positive and negative electrode potentials.

Thermodynamically (consider for instance the Nernst equation), infinitely high or low electrode potentials are required to either fully discharge (delithiate) or charge (lithiate) an intercalating battery electrode, which on cell level would correspond to either infinitely high or low cell voltages for a completely charged or discharged battery. During normal operation, the cell voltage is limited, and the full host capacity (cs,max) of neither electrode is hence fully utilized. In addition, the integrated host capacities of the positive and negative electrodes typically differ in order to provide a safety margin in order to avoid parasitic reactions, for instance, lithium plating.

The state of charge (SOC) of a battery cell can be coupled to the concentration levels (cs) of the individual electrode materials starting with the definition of two voltage parameters: The cell voltage at 100% SOC,

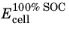
(V), and the cell voltage at 0% SOC,

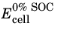
(V), which relate to the corresponding electrode potentials as

The cell voltage relations provide one equation for the two unknown positive and negative electrode potentials at each SOC level.

The second needed equation for defining Epos and Eneg (for any SOC level) can be derived by assuming conservation of the lithium inventory.

The concentration of intercalated lithium of an electrode at equilibrium, cs,eq (mol/m3) is a function of the electrode potential

Integrating the equilibrium concentration over the whole domain, Ω, where an electrode material is present, allows for computing the lithium inventory,

(C), for the corresponding potential at equilibrium

Finally, the second needed equation is found by setting the sum of the positive and negative lithium inventories at equilibrium equal to the total amount of lithium in the cell, Qinv,cell:

Once the electrode potentials at 0% and 100% SOC are known, the battery capacity, Capcell (C), can be defined as

Here the superscripts and subscripts indicate which cell state of charge, electrode, and potential

that are evaluated.

Subsequently, the cell state of charge, SOC (1), can be defined as

As a battery ages, Epos and Eneg at 0% and 100% SOC may change as a result of changes in the total inventory and/or the electrode volume fractions. This will give rise to a changing capacity. The fraction of the present capacity to the initial capacity defines the state of health, SOH (1), as

Common in battery engineering is to define the battery current in terms of C rates, where a 1C rate corresponds to the (ideal) time required to discharge the battery in 1 hour. The 1C current, I1C (A), may hence be calculated as

Note by this definition of the 1C current, polarization losses (originating from, for example, mass transport and electrochemical reaction limitations) are not accounted for. Usually a battery cell will not be able to support the 1C current for the whole course of an hour.

The framework in the above section can also be used to define the initial concentration levels in intercalating electrodes based on an initial cell voltage or cell SOC. For both cases, an initial cell inventory Qinv,cell,0 (C) parameter is required as user input.

When defining an initial cell voltage, Ecell,init, the corresponding initial electrode potentials, Epos,init and Eneg,init, are determined from the relations

When defining the cell state of charge, SOC0 (1), the second relation above is used similarly in combination with

and

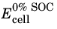
in order to define the initial potentials at 0% and 100% SOC, and the initial potentials are in turn calculated using the relations

The electrode host material can undergo significant volume changes during charging and discharging. If concentration gradients are present in the electrode particles, resulting in inhomogeneous elastic deformation, this will give rise to stresses.

Since atomic diffusion in solids is a much slower process than elastic deformation, mechanical equilibrium is established much faster than that of diffusion. Hence, mechanical equilibrium can be treated as a static equilibrium problem. In the analysis below, the electrode particles (spheres or cylinders) are assumed to be isotropic linear elastic solids.

The relative change in volume δV/V0 is typically dependent on the solid phase concentration cs (or the state-of-charge variable soc). Note that cs is solved for in a 1D extra dimension using spherical or cylindrical coordinate systems (for spheres or cylinders, respectively), as described above. In the equations presented below, the relative volume change is considered to be a generic function of the concentration ΔV/V0 = fvol(cs(r)).

The relationships between stress, σ(r) (SI unit: Pa), and strain, ε(r) (SI unit: 1), expressed in the spherical coordinate system for the radial and tangential components (considering that σθ(r) = σϕ(r)) are

where E (SI unit: Pa) is Young’s modulus and ν (SI unit:1) is Poisson’s ratio. It is assumed that these elastic properties are independent of concentration.

The expressions for radial and tangential stresses in a spherical particle of radius rp that satisfy the boundary condition σr(rp) = 0 and remain finite at r = 0, can be obtained as follows, by solving the equation for static mechanical equilibrium in the absence of any body force:

where the two integrals represent contributions, respectively, one given by an integral over the entire volume of the spherical particle and another given by an integral over a spherical volume of radius r within the particle. Note, that the tangential component additionally contains a local term as given by the last term in the expression.

The hydrostatic stress σh(r) (SI unit: Pa) (or the mean stress) is given by

The von Mises stress σv(r) (SI unit: Pa) given by

Because of spherical symmetry, one principal shear stress is zero and the other two are both equal to (σr(r) − σθ(r))/2.

The strain energy density Ws(r) (SI unit: J/m3) accumulated as a result of the elastic deformation for the isotropically deformed sphere is given as

The total elastic strain energy density stored in the host electrode material Ws,tot(r) (SI unit: J/m3), which provides the driving force for fracture, is obtained as,

where εs is the electrode volume fraction in the host material.

The relationships between stress, σ(r), and strain, ε(r), expressed in the cylindrical coordinate system for the radial, tangential, and axial components are as follows:

The expressions for radial, tangential, and axial diffusion-induced stresses for a transversely isotropic cylindrical particle of radius rp are

The hydrostatic stress σh(r) is given by

The von Mises stress σv(r) is given by

The strain energy density Ws(r) accumulated as a result of the elastic deformation for the isotropically deformed cylinder is given as

The total elastic strain energy density stored in the host electrode material Ws,tot(r) is given as

The material balance for the electrolyte salt concentration in porous media with convection included is normally written as

where Jl denotes the molar flux relative to the convective transport, u the solvent velocity vector, and Rl the total Li+ source term. The above formulation is referred to as the nonconservative form.

With the conservative form of the material balance as starting point and considering typical solvent properties, it can be shown that the nonconservative form can often describe the electrolyte salt concentration well.

The conservative form of the material balance is formulated as

The material balance of the solvent species in the battery can be written as

where R0 is the sum molar sources and sinks of the solvent species.

The above formulation can be rearranged to

The above relation may be used to rewrite the material balance of the salt to

Assuming the source term as well as the time and spatial derivatives of the solvent to be negligible in relation to the total concentration, the salt material balance may be simplified into its nonconservative form.

Porosity changes generally induce convection in the cell. However, since the convective contributions to the salt mass transfer from the fluid movement are usually small, the convective electrolyte transport is still often neglected in such models. For the combination of porosity changes and neglected convective transport, the choice of equation form will however not be arbitrary, and will render different results.

If porosity changes result mainly due to structural effects, such as expansion of an electrode material upon lithiation, with no associated loss of total amount of salt in the cell, the nonconservative form will avoid introducing artificial source terms due to nonzero time derivatives of the porosity. The conservative form on the other hand will conserve the total amount of salt (electrolyte ions) in the model, which could sometimes be preferable.

The logarithm formulation of the electrolyte salt concentration can be beneficial for convergence in models featuring salt depletion, for instance cells running at high current loads.

The electrolyte current density vector is defined as

For the case of a net-zero current vector in the absence of source terms, this results in the following relation between the gradients in potential and concentration:

In the limit of low concentrations, the activity coefficient and transport number will approach constant values, resulting in

By solving for the logarithm of the salt concentration, lncl, as dependent variable, instead of the concentration itself, the numerically unstable division by zero is inherently avoided. In addition, spurious oscillations in the equation residuals are avoided.