Surrogate Models — Polynomial Chaos Expansion

Polynomial chaos expansion (PCE) is an efficient surrogate model that provides approximations to the QoIs using a spectral representation on a basis of polynomial functions with respect to the input parameter distributions. Consider a model represented by y = M(x). Here, x is the vector of input parameters, and y is the vector of QoIs. For a vector-valued y, one PCE is computed for each QoI. For clarity, a scalar y is considered from now on. The input parameters x are independent variables with a prescribed PDF f(x). The QoI, y, can be expanded into an orthonormal polynomial basis,

Here, aα are unknown coefficients, and ψα are multivariate polynomials. For input parameters of each distribution type, there is a family of orthonormal polynomials,

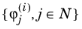
, in terms of which the multivariate polynomial ψα is defined as

where α is a multidimensional index, and m is the dimension of input parameters.

The classical family of univariate orthonormal polynomials and the distributions to which they are orthonormal are given in Table 2-1.

Table 2-1: List of classical polynomial families for polynomial chaos expansion.
Input Parameter distribution	Expression	Polynomial family
Uniform	x/2, x ∈ [−1, 1]	Legendre
Normal	exp(−x2/2)/(2π), x ∈ [−∞, ∞]	Hermite
Gamma	exp(−x)xα/Γ(α + 1), x ∈ [0, ∞]	Laguerre
Beta	(1 − x)α(1 + x)β/B(α + 1, β + 1), x ∈ [−1, 1]	Jacobi

In case the input parameters do not have a distribution given in the table, the algorithm defines an isoprobabilistic transformation to a uniform distribution and builds the PCE with the transformed input parameter. Further details about the orthonormal polynomial bases can be found in Ref. 5. Given the definition of the PCE, a truncation is defined such that the total degree of all polynomials is less than or equal to p. In addition, a hyperbolic truncation scheme that uses a parametric q-norm, q ∈ [0, 1], is used to further truncate the polynomial expansions. For q = 1, the truncation method truncates all polynomials with total degrees smaller than p. For q < 1, hyperbolic truncation includes all the high-degree terms in each input parameter, but it removes equivalently high-order interaction terms. For q = 0, the truncation method truncates all interaction terms between input parameters. A sparse representation of PCE refers to a sparsely selected polynomial basis from all the truncated polynomial expansions. An adaptive algorithm based on a least-angle regression method is used to select the significant sparse coefficients from all the truncated polynomial expansions. During the iterative process, the algorithm only adds new polynomial bases that are most correlated with the residual built with the existing polynomial basis. The sparse representation is both used for reducing the computational cost and, more importantly, for avoiding overfitting. Here, the leave-one-out cross-validation error estimation is defined with a correction factor that is used to consider overfitting and ensure that the generalization error estimate is not underestimated. The generalization error refers to the error for the sample points with unknown model evaluations. Additional details on the sparse PCE representation and the error estimation can be found in Ref. 6.

In COMSOL Multiphysics, both SPCE and ASPCE are trained adaptively based on the maximum total degree p. For ASPCE, the q-norm is also learned adaptively. Meanwhile, depending on whether the a posteriori cross-validation error estimation satisfies the tolerance, the ASPCE adds more input points selected by sequential optimal LHS to compute more model evaluations and train a new PCE in every adaptive step. For both SPCE and ASPCE, the truncated sparse coefficients are computed with an ordinary-least-square method in each adaptive step. You can use a specified q-norm for sparse PCE. If you have a priori information that the input parameter interaction is limited, a lower q-norm can be used to reduce the risk of overfitting.