You are viewing the documentation for an older COMSOL version. The latest version is
available here.
The term shape memory alloy (SMA) normally refers to alloys that can undergo large strains, effect called
superelasticity or
pseudoelasticity; and also to materials that after undergoing large deformations can remember their original shape when heated above a certain temperature, so-called
memory effect.
Hot NiTi alloys are composed by a pure austenite phase. The martensite phase develops upon cooling the alloy below the martensite start temperature,
Ms. The martensite volume fraction
ξM will increase until the cooling temperature reaches the
martensite finish temperature,
Mf, below which the alloy microstructure will be pure martensite.
The reverse process has different transition temperatures: A pure martensite alloy will develop an austenite microstructure if it is heated above the austenite start temperature,
As. The austenite phase will increase upon heating the material to the
austenite finish temperature,
Af, above which the alloy microstructure becomes 100% austenite.
Here, c is the heat capacity at constant pressure,
K and
G are the bulk and shear moduli,
εvol is the volumetric strain,
Hk is the hardening modulus, and
I(
εtr) is the
indicator function for the strain limit constraint. The
equivalent transformation strain εtre is used as a measure of the transformation strain tensor
The term ψch = τm(T)|εtr| is denoted as the chemical energy density due to the thermally induced martensite transformation. The function
τm(T) corresponds to the temperature-dependent martensite to austenite equilibrium stress, defined from the slope of the limit curve
β and the reference temperature
T*
Here, the operator < > denotes the Macaulay brackets.
The conjugated thermodynamic stress σtr associated to the transformation strain variable is
(3-145)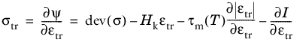
The evolution of the transformation strain εtr is given by the so-called
limit function, which takes the same form as the yield function for von Mises plasticity.
where σ0 is the
elastic domain radius.
In Ref. 39 it was suggested to consider the asymmetric behavior that many alloys show in tension and compression. In this case, the
limit function depends on the Lode angle
θ, the elastic radius in tension
σt, and elastic radius in compression
σc.
Denoting the elastic domain radius in tension
σ0 = σt, and the compression to tension stress ratio
k such as
σc = kσt = kσ0, the asymmetric
limit function reads
In Ref. 39, the stability for the limit function
Fy is achieved when
k ≤ 1.286.
where the plastic multiplier λp is solved with the Kuhn–Tucker conditions, as done for plasticity, see
Plastic Flow for Additive Decomposition.
where F is the total deformation gradient. See also
Plastic Flow for Multiplicative Decomposition. The last three terms in
Equation 3-145 can, moreover, be recognized as the back stress in a linear kinematic hardening model. Hence the framework for kinematic hardening with
Multiplicative Decomposition is used.
For Lagoudas model, Gibbs free energy density depends on two state variables: the total stress tensor σ and the temperature field
T. Additional internal variables are used to compute the transformation strain tensor
εtr and the martensite volume fraction
ξ (
Ref. 41)
Here, c is the heat capacity at constant pressure,
s0 is the specific entropy at reference state,
S is the compliance matrix,
εth is the thermal strain tensor,
εtr is the transformation strain tensor,
u0 is the specific internal energy at reference state, and
f(
ξ) is the
transformation hardening function. The compliance matrix
S, is obtained by a volume average of the elastic properties of martensite and austenite
where ΔS = SM − SA. Also, other material parameters are averaged this way.
where the normalized transformation tensor Λ changes principal directions depending on the direction of the martensitic transformation.
The maximum transformation strain in Lagoudas model can be considered constant, or stress-dependent as described in Ref. 42. A stress-dependent maximum transformation strain can be used at low stress levels, where the martensite turns into detwinned structures.
The variable for the direction of the martensitic transformation, 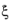 , is calculated from the previous state to determine the expected increment or decrement of the transformation strain tensor εtr
, is calculated from the previous state to determine the expected increment or decrement of the transformation strain tensor εtr. This calculation is computational expensive and it can lead to convergence issues. Since in many applications the transformation direction
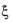
is known a priori (for instance, mechanical loading or unloading, or temperature increment/decrement) a user input enables to set the transformation direction manually to 1 or -1, thus speeding up the computational time.
where the parameters bM and
bA are computed from
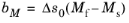 and
and 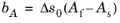
,
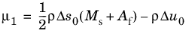 and
and 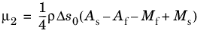
When the experimental data consists of a uniaxial stress-strain curve taken at a constant temperature Tσ above the austenite finish temperature
Af, it is possible to observe the
pseudoelastic or
superelastic effect. In this case it is convenient to enter the transition stress levels instead of the transition temperatures since these are easily derived from the uniaxial curve.
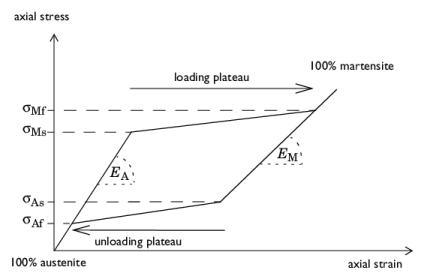
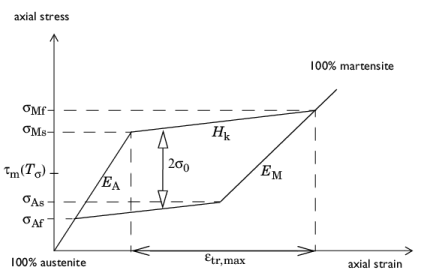
Consider a NiTi alloy composed by 100% of austenite at room temperature Tσ>Af. Upon loading, the slope in the stress-strain curve would be the Young’s modulus of austenite,
EA. The martensite phase starts to develop when the axial stress reaches the
martensite start stress,
σMs. If the alloy is further loaded, the slope reduces, entering a region called
loading plateau. Above the
martensite finish stress,
σMf, the microstructure becomes 100% martensite. This process is commonly called the
forward transformation.
The reverse process has different transition stresses: When the 100% martensite alloy is unloaded at constant temperature Tσ>Af, the slope follows the martensite Young’s modulus
EM. When the axial stress reaches the
austenite start stress,
σAs, the austenite volume fraction
ξA starts to develop until the axial stress falls below the
austenite finish stress,
σAf, at which level the alloy microstructure is 100% austenite. This process is commonly called the
reverse transformation.
Figure 3-30 illustrates this process.
here, Tσ is the constant temperature at which the stress-strain curve for the pseudoelastic effect was measured. This curve is observed when the temperature
Tσ is higher than the austenite finish temperature
Af.
The two slopes of austenite and martensite limit curves CA and
CM are sometimes referred to as the
Clausius-Clapeyron constants are measured in a strain-temperature curve at constant stress (
Ref. 41).
Lagoudas model contains more parameters than the Souza–Auricchio model. The latter model assumes that the slope of limit curves to martensite and austenite are equal, this is, CM = CA. These two parameters influence the slopes of the loading and unloading plateaus, respectively. For the Souza–Auricchio model, the slope of limit curve
β can be taken from the martensite limit curve
CM, or as the average between the austenite and martensite limit curves.
The function τm(T) corresponds to the temperature-dependent martensite to austenite equilibrium stress. It is defined from the slope of the limit curve
β and the reference temperature
T*. At the current temperature
Tσ it equals
The elastic radius σ0 represents half of the height of the hysteresis loop, and it depends on the temperature at which the superelastic effect was measured
The hardening parameter Hk relates the slope in the loading plateau with the difference between the
martensite finish stress,
σMf, and the
martensite start stress,
σMs
here, εtr,max is the maximum transformation strain measured in a strain-temperature curve at constant stress (
Ref. 40).
The Souza–Auricchio model assumes that the width of the transition zones in the phase diagram are equal, that is, the temperature difference Af − As and
Ms − Mf are the same, which is not the case in the Lagoudas model. In the Souza–Auricchio model, the reference temperature
T* is taken as the average temperature between the martensite start temperature and the austenite finish temperature
Considering, CM = CA = β, it is possible to write the reference temperature
T* in terms of the martensite start stress, the austenite finish stress, and the measurement temperature
Tσ
Figure 3-31 illustrates the material parameters for the Souza–Auricchio model.
As plasticity is rate independent, the transformation dissipation density Wtr is obtained after integrating an extra variable in the plastic flow rule.
|
|
When the Calculate dissipated energy check box is selected, the transformation dissipation density is available under the variable solid.Wtr and the total transformation dissipation under the variable solid.Wtr_tot.
|

